


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-4-2022
Date: 20-5-2022
Date: 10-5-2022
|
We begin this section with a simple question: How many people are required at a gathering so that there must exist either three mutual acquaintances or threemutual strangers? We will answer this question soon. Ramsey theory is named for Frank Ramsey, a young man who was especially interested in logic and philosophy.
Ramsey died at the age of 26 in 1930—the same year that his paper On a problem of formal logic was published. His pa-per catalyzed the development of the mathematical field now known as Ramsey theory. The study of Ramsey theory has burgeoned since that time. While many results in the subject are published each year, there are many questions whose answers remain elusive. As the authors of [2] put it, “the field is alive and exciting.”
"Ramsey theory" refers to the study of partitions of large structures. Typical results state that a special substructure must occur in some class of the partition. Motzkin described this by saying that "Complete disorder is impossible". The objects we consider are merely sets and numbers, and the techniques are little more than induction. Ramsey's Theorem" generalizes the pigeonhole principle, which itself CQllcerns partitions of sets. We study applications of the pigeonhole principle, prove Ramsey's Theorem, and then focus on Ramsey-type questions for graphs. Finally, we discuss Sperner's Lemma about labelings of triangulations; "like Ramsey's Theorem, it guarantees a special substructure.[3]
Classical Ramsey Numbers
A 2-coloring of the edges of a graph G is any assignment of one of two colors to each of the edges of G. Figure 1.1 shows a 2-coloring of the edges of K5 using red (thick) and blue (thin).
Let p and q be positive integers. The (classical) Ramsey number associated with these integers, denoted by R(p, q), is defined to be the smallest integer n such that every 2-coloring of the edges of Kn either contains a red Kp or a blue Kq as a subgraph.
Read through that definition at least one more time, and then consider this simple example. We would like to find the value of R(1, 3). According to the definition, this is the least value of n such that every 2-coloring of the edges of Kn

FIGURE 1.1. A 2-coloring of K5.
either contains as a subgraph a K1 all of whose edges are red, or a K3 all of whose edges are blue. How many vertices are required before we know that we will have one of these objects in every coloring of a complete graph? If you have just one vertex, then no matter how you color the edges (ha-ha) of K1, you will always end up with a red K1. Thus, R(1, 3) = 1.We have found our first Ramsey number!
We should note here that the definition given for Ramsey number is in fact a good definition. That is, given positive integers p and q, R(p, q) does in fact exist. Ramsey himself proved this fact, and we will learn more about the proof of “Ramsey’s Theorem”.
Back to examples. We just showed that R(1, 3) = 1. Similar reasoning shows that R(1,k)=1 for all positive integers k .
How about R(2, 4)?We need to know the smallest integer n such that every 2- coloring of the edges of Kn contains either a red K2 or a blue K4. We claim that R(2, 4) = 4. To show this, we must demonstrate two things: first, that there exists a 2-coloring of K3 that contains neither a red K2 nor a blue K4, and second, that any 2-coloring of the edges of K4 contains at least one of these as a subgraph. We demonstrate the first point. Consider the 2-coloring of K3 given in Figure 1.2 (recall that red is thick and blue is thin—the edges in this coloring are all blue). This coloring of K3 does not contain a red K2, and it certainly does not

FIGURE 1.2. The edges of K3 colored blue.
contain a blue K4. Thus R(2, 4) > 3.
For the second point, suppose that the edges of K4 are 2-colored in some fashion. If any of the edges are red, then we have a red K2. If none of the edges are red, then we have a blue K4. So, no matter the coloring, we always get one of the two. This proves that R(2, 4) = 4.
What do you think is the value of R(2, 5)? How about R(2, 34)? As you will prove in Exercise 3, R(2,k)= k for all integers k ≥ 2.
Exact Ramsey Numbers and Bounds
How many people are required at a gathering so that there must exist either three mutual acquaintances or three mutual strangers? We can rephrase this question as a problem in Ramsey theory: How many vertices do you need in an (edge) 2-colored complete graph for it to be necessary that there be either a redK3 (people who know each other) or a blue K3 (people who do not know each other)? As the next theorem states, the answer is 6.
Theorem 1.1. R(3, 3) = 6.
Proof. We begin the proof by exhibiting (in Figure 1.3) a 2-coloring of the edges of K5 that produces neither a red (thick) K3 nor a blue (thin) K3.This
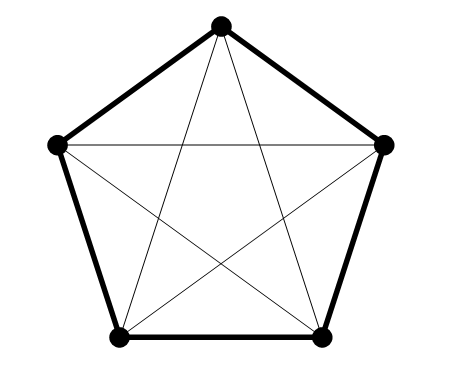
FIGURE 1.3. A 2-coloring of the edges of K5.
2-coloring of K5 demonstrates that R(3, 3) > 5. Now consider K6, and suppose that each of its edges has been colored red or blue. Let v be one of the vertices of K6. There are five edges incident with v, and they are each colored red or blue, so it must be that v is either incident with at least three red edges or at least three blue edges (think about this; it is called the Pigeonhole Principle—more on this in later chapters).Without loss of generality, let us assume that v is incident with at least three red edges, and let us call them vx, vy,and vz (see Figure 1.4).

FIGURE 1.4.

FIGURE 1.5.
Now, if none of the edges xy, xz, yz is colored red, then we have a blue K3 (Figure 1.5).
On the other hand, if at least one of xy, xz, yz is colored red, we have a red K3 (Figure 1.6).
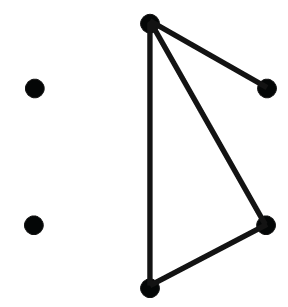
FIGURE 1.6.
Therefore, any 2-coloring of the edges ofK6 produces either a red K3 or a blue K3.
Let us determine another Ramsey number.
Theorem 1.2. R(3, 4) = 9.
Proof. Consider the 2-coloring of the edges of K8 given in Figure 1.7. A bit of examination reveals that this coloring produces no red (thick) K3 and no blue (thin) K4. Thus, R(3, 4) ≥ 9. We now want to prove that R(3, 4) ≤ 9, and we will use the facts that R(2, 4) = 4 and R(3, 3) = 6.
Let G be any complete graph of order at least 9, and suppose that the edges of G have been 2-colored arbitrarily. Let v be some vertex of G.
Case 1. Suppose that v is incident with at least four red edges. Call the end vertices of these edges “red neighbors” of v, and let S be the set of red neighbors of v (see Figure 1.8).

FIGURE 1.7. A 2-coloring of the edges in K8.
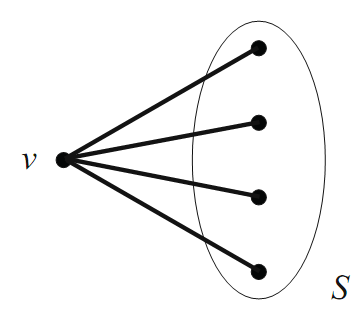
FIGURE 1.8.
Since S contains at least four vertices, and since R(2, 4) = 4, the 2-coloring of the edges that are within S must produce either a red K2 or a blue K4 within S itself. If the former is the case, then we are guaranteed a red K3 in G (see Figure 1.9). If the latter is the case, then we are clearly guaranteed a blue K4 in G.

FIGURE 1.9.
Case 2. Suppose that v is incident with at least six blue edges. Call the other end vertices of these edges “blue neighbors” of v, and let T be the set of blue neighbors of v (see Figure 1.10). Since T contains at least six vertices, and since R(3, 3) = 6, the 2-coloring of the edges that are within T must produce either a red K3 or a blue K3 within T itself. If the former is the case, then we are obviously guaranteed a red K3 in G.

FIGURE 1.10.
If the latter is the case, then we are guaranteed a blue K4 in G (see Figure 1.11).

FIGURE 1.11.
Case 3. Suppose that v is incident with fewer than four red edges and fewer than six blue edges. In this case there must be at most nine vertices in G altogether, and since we assumed at the beginning that the order of G is at least 9, we can say that G has order exactly 9. Further, we can say that v is incident with exactly three red edges and exactly five blue edges. And since the vertex v was chosen arbitrarily, we can assume that this holds true for every vertex of G.
Now if we consider the underlying “red” subgraph of G, we have a graph with nine vertices, each of which has degree 3. But this cannot be, since the number of vertices in G with odd degree is even (the First Theorem of Graph Theory). Therefore, this case cannot occur.
We have therefore proved that any 2-coloring of the edges of a complete graph on 9 vertices (or more) produces either a red K3 or a blue K4. Hence, R(3, 4) = 9.
Some known Ramsey numbers are listed below.

Bounds on Ramsey Numbers
Determining exact values of Ramsey numbers is extremely difficult in general. In fact, the list given above is not only a list of some known Ramsey numbers, it is a list of all known Ramsey numbers. Many people have attempted to determine other values, but to this day no other numbers are known.
However, there has been progress in finding bounds, and we state some important ones here. The first bound is due to Erd o˝s and Szekeres [4], two majorplayers in the development of Ramsey theory. Their result involves a quotient of factorials: Here, n! denotes the product 1 · 2 ··· n.
Theorem 1. 3. For positive integers p and q,
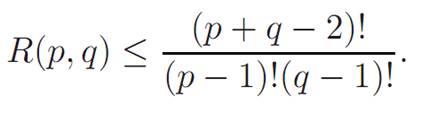
The next theorem gives a bound on R(p, q) based on “previous” Ramsey numbers.
Theorem 1.4. If p ≥ 2 and q ≥ 2,then

Furthermore, if both terms on the right of this inequality are even, then the in- equality is strict. The following bound is for the special case p =3.
Theorem 1.4. For every integer q ≥ 3,
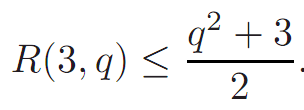
The final bound that we present is due to Erd o˝s [5]. It applies to the special case p = q.In the theorem, |x| denotes the greatest integer less than or equal to x.
Theorem 1.5. If p ≥ 3,then

A number of other specific bounds are known:
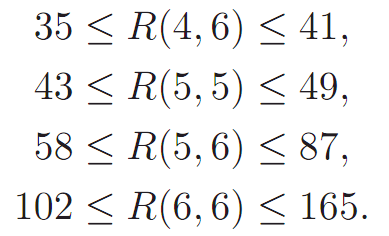
Even with the sophisticated computing power that is available to us today, we are not able to compute values for more than a handful of Ramsey numbers.
Paul Erdo˝ s once made the following comment regarding the difficulty in finding exact values of Ramsey numbers [6]:
Suppose an evil alien would tell mankind “Either you tell me [the value of R(5, 5)] or I will exterminate the human race.” . . . It would be best in this case to try to compute it, both by mathematics and with a computer.
If he would ask [for the value of R(6, 6)], the best thing would be to destroy him before he destroys us, because we couldn’t [determine R(6, 6)].
Graph Ramsey Theory
Graph Ramsey theory is a generalization of classical Ramsey theory. Its development was due in part to the search for the elusive classical Ramsey numbers, for it was thought that the more general topic might shed some light on the search. The generalization blossomed and became an exciting field in itself. In this section we explain the concept of graph Ramsey theory, and we examine several results. These results, and more like them, can be found in [2].
Given two graphs G and H, define the graph Ramsey number R(G,H) to be the smallest value of n such that any 2-coloring of the edges of Kn contains either a red copy of G or a blue copy of H. The classical Ramsey number R(p, q) would in this context be written as R(Kp,Kq). The following simple result demonstrates the relationship between graph Ramsey numbers and classical Ramsey numbers.
Theorem 1.6.
If G is a graph of order p and H is a graph of order q, then

Proof. Let n = R(p, q), and consider an arbitrary 2-coloring of Kn.By definition ,Kn contains either a red Kp or a blue Kq. since G ⊆ Kp and H ⊆ Kq, there must either be a red G or a blue H in Kn. Hence, R(G,H) ≤ n = R(p, q). Here is a result due to Chva´ tal and Harary [7] that relates R(G,H) to the chromatic number of G, χ(G), and the order of the largest component of H, denoted by C(H).
Theorem 1.7. R(G,H) ≥ (χ(G) − 1)(C(H) − 1) + 1.
Proof. Let m = χ(G) − 1 and let n = C(H) − 1. Consider the graph S formed by taking m copies of Kn and adding all of the edges in between each copy (Figure 1.13). Actually, S = Kmn. Now color all of the edges within each Kn blue, and color all other edges red. From the way we have constructed the coloring, every red subgraph can be vertex colored with m colors. Since m< χ(G), there can be no red G present. Furthermore, any blue subgraph has at most n = C(H) − 1 vertices in its largest component. Hence, there can be no blue H present. We have exhibited a 2-coloring of Kmn that contains neither a red G nor ablue H.

FIGURE 1.12. The graph S.
The next few theorems give exact graph Ramsey numbers for specific classes of graphs. The first is due to Chva´ tal [8], and the proof uses a few ideas from previous sections.
Theorem 1.8. If Tm is a tree with m vertices, then

Proof. If m =1 or n =1,then R(Tm,Kn)=1 and the result holds. Assume then that m and n are both at least 2.

Consider the graph that consists of n−1 copies of Km−1, with all possible edges between the copies of Km−1. This graph is actually K(m−1)(n−1). Color the edges in each Km−1 red, and color all of the other edges blue. Since each of the red subgraphs has order m − 1,nored Tm can exist. Also, by this construction, no blue Kn can exist. Since this 2-coloring contains no red Tm and noble Kn, it must be that


Let G be K(m−1)(n−1)+1, and suppose that its edges have been arbitrarily 2- colored. Let Gr denote the subgraph of G formed by the red edges, and let Gb denote the subgraph of G formed by the blue edges. If there is no blue Kn, then ω(Gb) ≤ n−1, and if so, then α(Gr) ≤ n−1,since Gr is the complement of Gb.
The next theorem is due to Burr [9].
Theorem 1.9. If Tm is a tree of order m and if m− 1 divides n − 1,then

In the following theorem, mK2 denotes the graph consisting of m copies of K2,and nK2 has a similar meaning.
Theorem 1.10.
If m ≥ n ≥ 1,then

As we mentioned earlier, these results apply to specific classes of graphs. In general, determining values of R(G,H) is quite difficult. So the generalization that was intended to solve hard classical Ramsey problems has produced hard problems of its own!
1-Combinatorics and Graph Theory, Second Edition, John M. Harris • Jeffry L. Hirst • Michael J. Mossinghoff,2000,page(116-126)
2- R. L. Graham, B. L. Rothschild, and J. H. Spencer, Ramsey Theory, 2nd ed., Wiley-Intersci. Ser. Discrete Math. Optim., John Wiley & Sons, New York, 1990.
3- Graph Theory and Applications ,Jean-Claude Fournier, WILEY, page(378)
4-P. Erd o˝s and G. Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935), 463–470; reprinted in I. Gessel and G.-C. Rota (eds.), Classic Problems in Combinatorics,
Birkha¨ user, Boston, 1987.
5-P. Erd˝ os, Some remarks on the theory of graphs, Bull. Amer. Math. Soc. 53 (1947), 292–294.
6-G. P. Csicsery (director), N is a Number: A Portrait of Paul Erd˝ os, Zala Films, Oakland, CA, 1993. Documentary film.
7-V. Chv´ atal and F. Harary, Generalized Ramsey theory for graphs III: Small off-diagonal numbers, Pacific J. Math. 41 (1972), no. 2, 335–345.
8-V. Chva´ tal, Tree-complete graph Ramsey numbers, J. Graph Theory 1 (1977), no. 1, 93.
9-S. A. Burr, Generalized Ramsey theory for graphs—A survey, Capital Conference on Graph Theory and Combinatory (George Washington Univ., Washington, DC, 1973), Graphs and
Combinatory (R. A. Bari and F. Harary, eds.), Lecture Notes in Math., vol. 406, Springer- Verlag, Berlin, 1974, pp. 52–75.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|