Period as Function of Energy

A particle of mass m moves in a one-dimensional potential U(x) = A |x|ⁿ  where A is a constant. Find the dependence of the period τ on the energy E in terms of n.

SOLUTION

Energy is conserved for a position dependent potential, so we may write E = (1/2) mẋ² + A |x|ⁿ. The time for a particle to travel between two turning points of its motion τ₁ and τ₂ (where its kinetic energy is zero) is given by

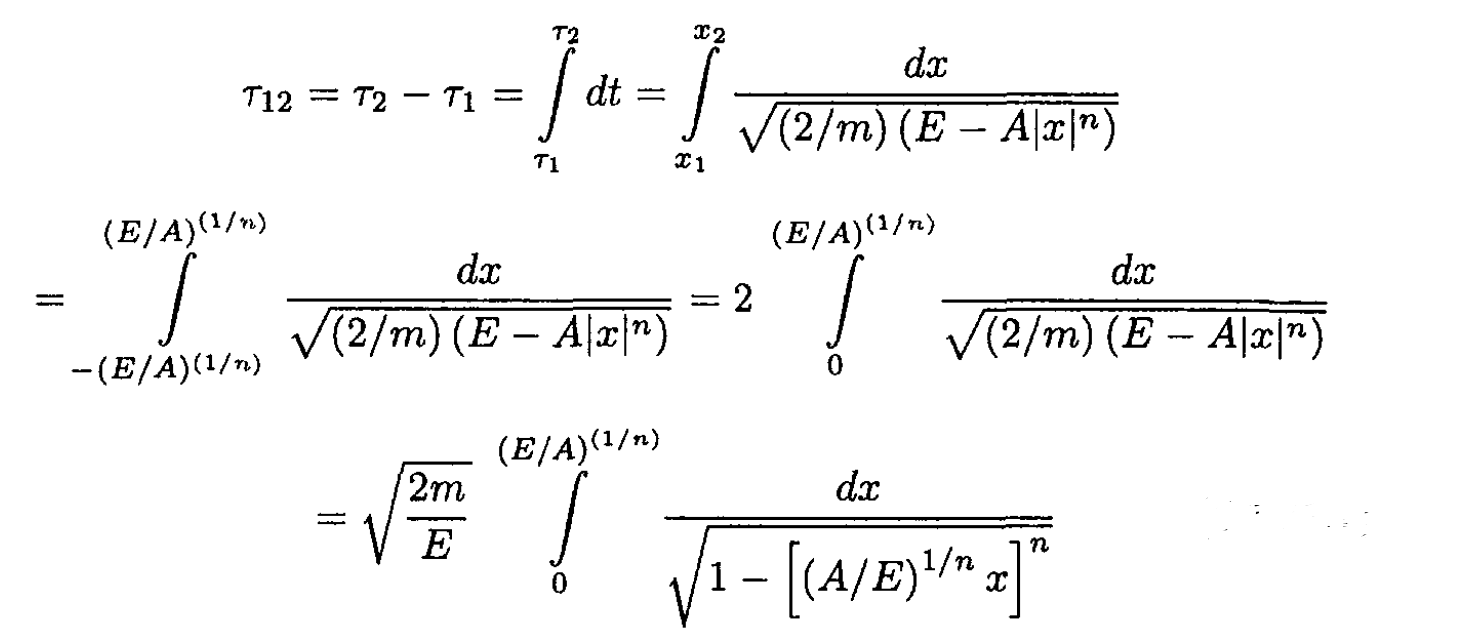(1)

Let u = (A/E)^1/n x. (1) then becomes

(2)

The period T is twice the time to go between points 1 and 2, T = 2τ₁₂. So for the energy dependence of the period, we have

(3)

For a harmonic oscillator n = 2, and  independent of E, as (3) confirms