Astronaut Tether

An astronaut of total mass 110 kg was doing an EVA (spacewalk, see Figure 1.1) when his jetpack failed. He realized that his only connection to

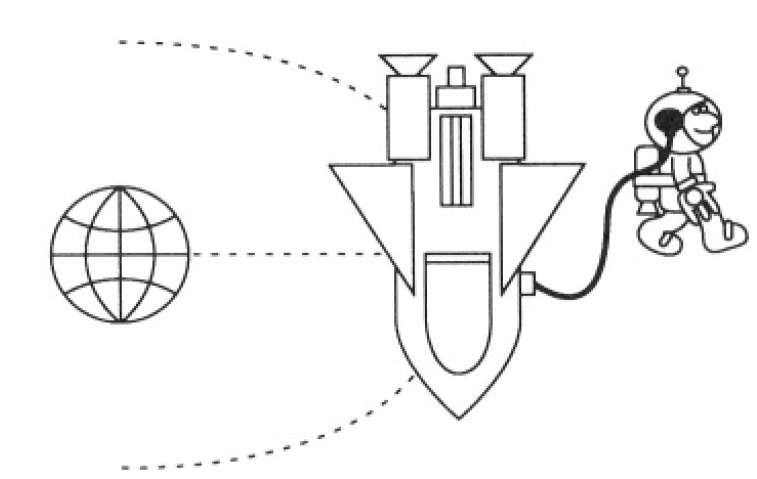
 Figure 1.1

 the spaceship was by the communication wire of length L = 100 m. It can support a tension of only 5 N before parting. Estimate if that is enough to keep him from drifting away from the spaceship. Assume that the height of the orbit is negligible compared to the Earth's radius (R = 6400 km). Assume also that the astronaut and the spaceship remain on a ray projecting from the Earth’s center with the astronaut further away from the Earth. 

SOLUTION

 The spaceship moves under the influence of the Earth’s gravity, given by

(1)     

where M is the mass of the spaceship, M_E is the Earth’s mass, R₁ is the distance between the center of the Earth and the ship, and G is the gravitational constant (see Figure 1.2). We may write for the spaceship

 Figure 1.2

(2)

where Ω is the angular velocity of the ship and T is the tension of the communication cable. Similarly, for the astronaut,

(3)

where m is the mass of the astronaut, R₂ is the radius of the orbit of the astronaut, and Ω is the angular velocity of his rotation about the Earth. Obviously, we can write (2) and (3) with the same angular velocity only for the specific case where the spaceship and the astronaut fall on a ray from the Earth’s center. Equating Ω from (2) and (3), we obtain

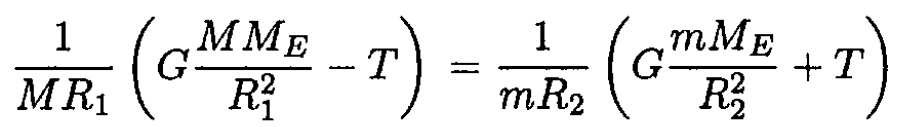(4)

From equation (4), we can easily find the tension T :

Using we R₁ ≈ R₂ ≈ R, R³₂ – R³₁ = (R₂ – R₁)(R²₂ + R₁R₂ + R²₁) ≈ 3R²L,  can rewrite T in the form:

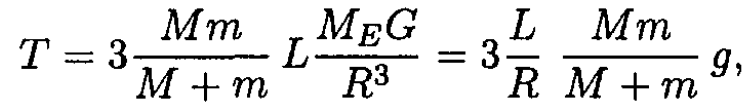
where is the acceleration on the surface of the Earth. Also, since M >> m, we can write an even simpler formula as an estimate:

Hence, the wire would withstand the tension of holding the hapless astronaut in tow.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين