
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Photon Box
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 34
13-7-2016
1455
Photon Box
An empty box of total mass M with perfectly reflecting walls is at rest in the lab frame. Then electromagnetic standing waves are introduced along the x direction, consisting of N photons, each of frequency v0 (see Figure 1.1).

Figure 1.1
a) State what the rest mass of the system (box + photons) will be when the photons are present.
b) Show that this answer can be obtained by considering the momentum and/or energy of the box-plus-photon system in any inertial frame moving along the axis.
SOLUTION
a) Consider the initial state of the system. Write the 4-momentum of the box and photons as pμbox and pμph, respectively:
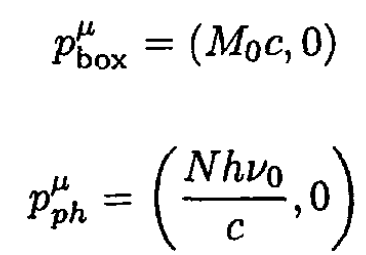 (1)
(1)
where we have used the fact that for a standing wave (which can be represented as the sum of traveling waves with opposite momenta) the total momentum is zero. Therefore, from (1), the 4-momentum of the system Pμ is given by
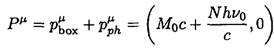 (2)
(2)
From (2), we can find the rest mass of the total system M (which is defined by M2 c2 = Pμ Pμ)
 (3)
(3)
b) Transform the 4-momentum by going into a frame moving with velocity –v along the x axis. We have in this frame for energy ε' and momentum P'
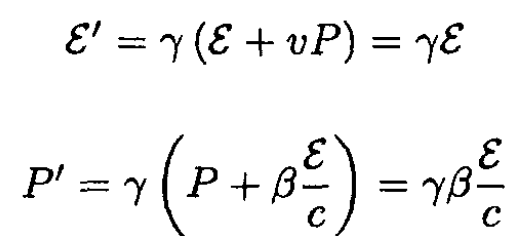
where ε and P are the total energy and momentum in the rest frame, respectively. So

Therefore in the moving frame

and

We expect this to be true, of course, since mass is a relativistic invariant under a Lorentz transformation.
Another way to look at it is to consider a transformation of energy and momentum of the photons and the box separately. The frequencies of these photons will be Doppler shifted:

The energy of the photons
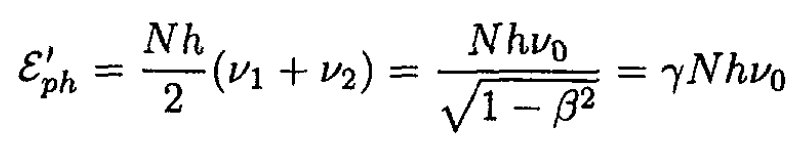
The energy of the box ε'box = γM0 c2. The momentum of the photons

The momentum of the box

So the 4-momentum is the same as found above

 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















