فضاء الصفوف وفضاء الأعمدة والفضاء الصفري:

نناقش في هذا البند بعض أنواع فضاء المتجهات وعلاقتها بالمصفوفات:

تعريف (1-1):

لتكن A مصفوفة سعتها m x n بالشكل:

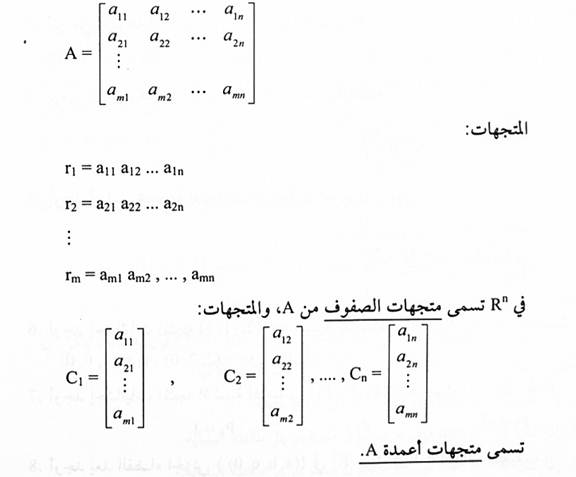
مثال(1):

لتكن 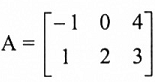فإن متجهات صفوف A هي:

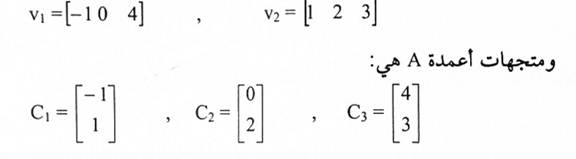
تعريف (1-2):

لتكن A مصفوفة سعتها m x n الفضاء   الجزئي فيR"  المتولد من متجهات صفوف A يسمى فضاء الصفوف والفضاء الجزئي من R" المتولد من متجهات أعمدة A يسمى فضاء الأعمدة, اما فضاء حل نظام المعادلات الخطية المتجانسة  AX = 0، والذي هو فضاء جزئي من R"، فيسمى الفضاء الصفري للمصفوفة A.

مثال(2):

في المثال(1) المجموعة {r₁, r₂} هي فضاء صفوف A و {c₁, c₂, c₃} هي فضاء أعمدة A.

مبرهنة (1-3):

يكون النظام AX = B قويماً (يحتوي على الأقل حل واحد) إذا وفقط إذا كان B موجوداً في أعمدة A.

البرهان: لتكن:

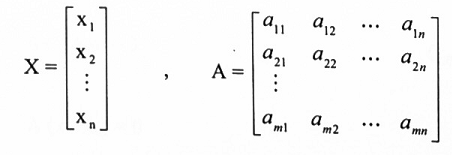
فإن من خواص ضرب المصفوفات يمكن كتابة AX بالشكل:

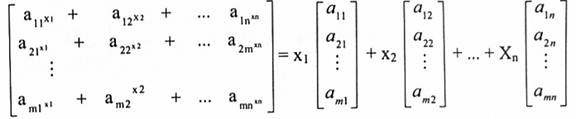
عليه فإن AX يمكن كتابته كتركيب خطي لمصفوفات أعمدة A اما المعاملات فهي من المصفوفة X.

لذا:

إذن النظام الخطي AX = B الذي يحتوي على m من المعادلات والتي تحتوي على n من المتغيرات يمكن التعبير عنه بالصيغة:

نستنتج من ذلك أن AX = B له على الأقل حل واحد إذا وفقط إذا أمكن التعبير عن B كتركيب خطي من أعمدة A، بمعنى آخر ، إذا وفقط إذا كانت B في فضاء أعمدة A.

مثال(3):

نفرض AX = B نظام خطي بالشكل الآتي. برهن أن B تنتمي لفضاء أعمدة A.

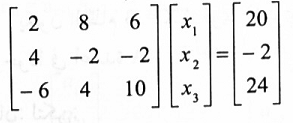
الحل:

باستخدام طريقة حذف كاوس (برهن ذلك) فإن:

          X₁ = 2          ،        X₂ = -1         ،        X₃ = 4

وبموجب المعادلة (2) نحصل على:

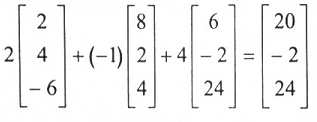
يتضح من هذا أن B تتمي لفضاء أعمدةA .

مبرهنة (1-4):

إذا كان X₀ يمثل أي حل للنظام الخطي القويم والغير متجانس AX = B  ولتكن v_n, … , v₂, v₁ أساس للفضاء الصفري في A، أي فضاء احل للنظام المتجانسAX = 0 ، فإن أي الحل للنظام يمكن كتابته بالشكل:

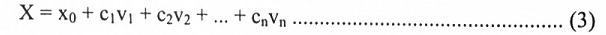
وبالعكس لكل اختيارات الثوابت c_n, … , c₂, c₁ فإن المتجه x في العلاقة (3) هو حل للنظام AX = B.

البرهان:

نفرض X₀ أي حل ثابت للنظام AX₀ = B و x أي حل لا على اليقين فإن:

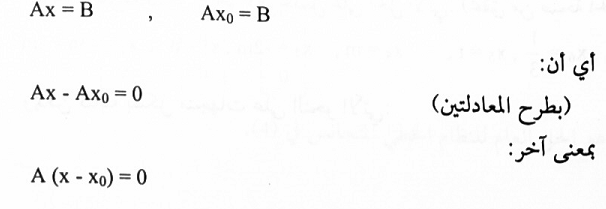
ومن هذه العلاقة نستنتج أن x - x_o هو حل للنظام المتجانس AX = 0

بما أن V_n, … , v₂, v₁ أساس فضاء الحل لهذا النظام فإن:

لكن x₀ هو حل للنظام غير المتجانس ولما كان v_n, … , v₂, v₁ هي حلول النظام المتجانس .لذا فإن المعادلة أعلاه ستكون:

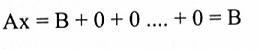
أي أن x هو حل للمعادلة AX = B.

مثال(4):

أوجد الحل العام للنظام الخطي غير المتجانس:

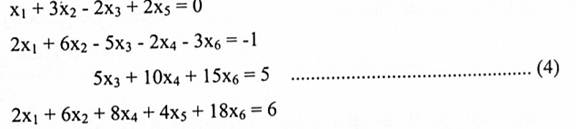
باستخدام طريقة كاوس ــ جوردان نحصل على الحل الآتي: (تحقق من صحة الحل)

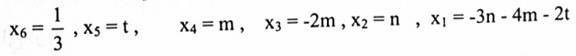
ويمكن كتابته بشكل متجهات على النحو الآتي:

هو الحل العام للنظام الخطي المتجانس في (4).

ملاحظة:

1. عمليات الصف البسيطة لا تغير الفضاء الصفري للمصفوفة وذلك لأننا لاحظنا في الفصل الأول أن العمليات الصفية البسيطة المستخدمة على المصفوفة الممتدة لا تبدل مجموعة حل النظام الخطي المقابل.

لذا فإن عمليات الصف البسيطة على المصفوفة A لا تبدل مجموعة حل النظام الخطي المقابل AX = 0، بمعنى آخر، لا تبدل الفضاء الصفري للمصفوفة A.

2. عمليات الصف البسيط لا تبدل فضاء الصفوف للمصفوفة نفرض أن متجهات صفوف A هي r_m, … , r₂, r₁ وأن B مصفوفة أمكن الحصول عليها من A بتطبيق عمليات الصف البسيطة على A. سوف نبين أن أي متجه من متجهات فضاء صفوف B هي داخل فضاء صفوف A. وبالعكس أي متجه في فضاء صفوف A هو داخل فضاء B. أي أننا نستطيع أن نقول أن B,A لهما نفس فضاء الصفوف. فلو افترضنا أن عملية الصف البسيطة هي تبديل الصفوف، فإن متجهات صفوف B هي نفسها متجهات صفوف A. لذا فإن A , B لهما نفس فضاء الصفوف، أما إذا كانت العملية الصفية البسيطة هي مضروب صف بكمية ثابتة او جمع مضروب صف مع صف آخر فإن متجهات صفوف B هي r'_n, …, r'₂, r'₁ عبارة عن تركيب خطي لمتجهات صفوف A وهي r_n, … , r₂, r₁ تقع في نفس فضاء صفوف A. لكن فضاء المتجهات هو معلق تحت عمليتي الجمع والضرب بكمية ثابتة، فإن جميع التركيبات الخطية للمتجهات r'_n, …, r'₂, r'₁ تقع في نفس فضاء متجهات A. لذا فإن أي متجه في فضاء صفوف B هو في فضاء صفوف A. وبما أن B يمكن الحصول عليها من A بتطبيق عملية صف بسيطة، فإن A يمكن الحصول عليها من تطبيق معكوس العملية. مما تقدم نستطيع القول بأن فضاء صفوف A محتواه داخل فضاء صفوف B.

3. من (1) و (2) يمكن للمرء أن يتوقع أن عمليات الصف البسيطة سوف لا تبدل فضاء أعمدة المصفوفة. وهذا ليس صحيحاً  فعلى سبيل المثال، إذا كانت

فإن العمود الثاني هو مضروب العمود الأول بكمية ثابتة، لذا فإن فضاء الأعمدة متكون من جميع مضروبات متجه العمود الأول بكمية ثابتة. بضرب الصف الأول بالعدد -2 وإضافته للصف الثاني سنحصل على 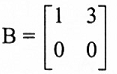، لاحظ ان العمود الثاني في B مضروب العمود الأول بكمية ثابتة أيضاً، لذا فإن فضاء الأعمدة B يتكون من جميع مضروبات متجه العمود الاول ولكن الفضاء ليس هو نفس فضاء أعمدة A.

لإيجاد طريقة نستطيع من خلالها معرفة أساسات فضاءات الصفوف والأعمدة لمصفوفة ما في الشكل المدرج الصفي فإن المبرهنة الآتية تعتبر مهمة بهذا الاتجاه.

مبرهنة (1-5):

لتكن R مصفوفة بالشكل المدرج الصفي، فإن متجهات الصفوف التي تحوي على الدليل 1 تكون فضاء صفوف R ومتجهات الأعمدة التي تحوي الدليل 1 تكون فضاء أعمدة R.

مثال(5):

أوجد اساسات فضاء الصفوف وفضاء الأعمدة للمصفوفة

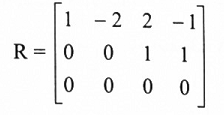
بما أن R بالشكل المدرج الصفي وبموجب (1-5) فإن المتجهات:

R2 = (00,1,1),  r1 = (1,-2,2,-1) أساس فضاء صفوف R والمتجهات

هي أساس فضاء أعمدة R.

مثال(6):

اوجد أساسات فضاء الصفوف وفضاء الأعمدة للمصفوفة:

لإيجاد أساس فضاء صفوف A نحول المصفوفة A للشكل المدرج الصفي ومن ثم نجد أساس فضاء صفوف الشكل المدرج الصفي الناتج.

وباختزال المصفوفة A للشكل المدرج الصفي باستخدام عمليات الصف البسيطة سنحصل على:

عليه فإن المتجهات:

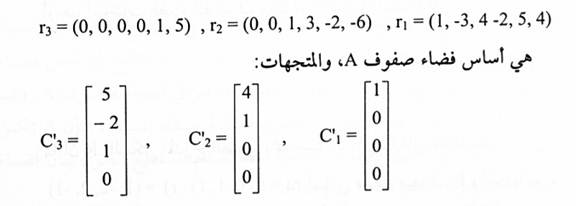
هي أٍساس فضاء أعمدة R. لذا فإن أعمدة A المقابلة لها هي:

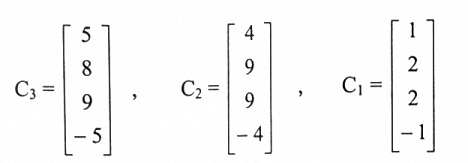
عليه فإن المتجهات C₃, C₂, C₁ تكون أساس فضاء أعمدة A.

مثال(7):

أوجد أساسات فضاء صفوف A وفضاء أعمدتها.

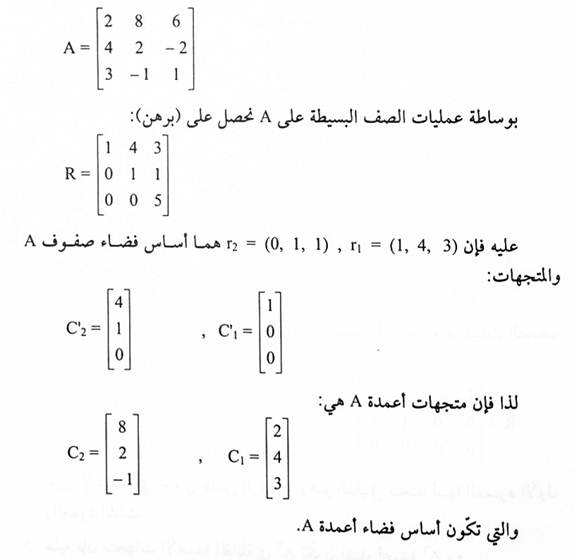
ملاحظة :

          لاحظنا في المثال(6) أن متجهات الأساس التي حصلنا عليها  لفضاء أعمدة A تتكون من متجهات أعمدة A، لكن متجهات الأساس التي حصلنا عليها لفضاء صفوف A لبست جميعها متجهات صفوف A.

الطريقة الآتية توضح كيفية إيجاد أساس فضاء صفوف المصفوفة A المتكونة تماماً من متجهات صفوف A.

مثال(8):

1. نفرض

4. نعين الأعمدة التي تحتوي على الرقم 1 وهو الدليل فنحد أنها العمود الأول والعمود الثالث.

5. عليه فإن متجهات الأعمدة المقابلة في A^T تكون فضاء أعمدة A^T وهي:

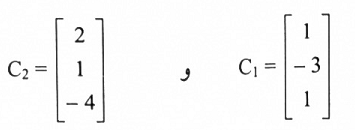
6. نجد المنقولة مرة ثانية فنحصل على متجهات الأساس لفضاء صفوف A وهي: