المصفوفات المتعامدة، تبديل الأساسات:

نتناول في هذا البند دراسة العلاقة بين مفهوم الأساس ومصفوفة الإحداثيات، وسندرس أيضاً طريقة تبديل أساسات فضاء المتجهات.

تعريف ((1-1:

يقال للمصفوفة المربعة A متعامدة إذا تحققت العلاقة:

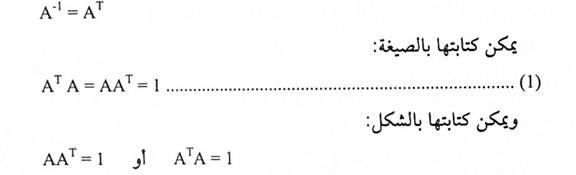
مثال(1):

برهن أن 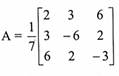 مصفوفة متعامدة. اوجد A^-1.

لما كان:

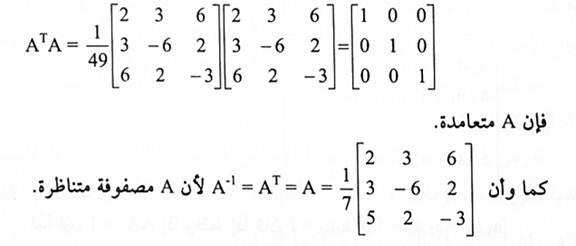
مثال(2):

المصفوفة الأساسية لدوران R² حول زاوية قيمتها θ هي:

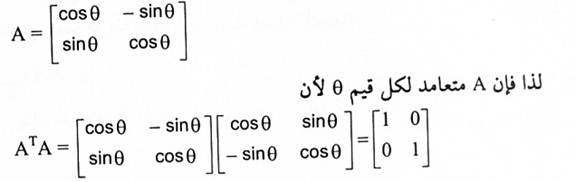
مبرهنة (1-2):

لتكن A مصفوفة سعتها n x n فإن الصيغ الآتية تكون متكافئة.

1. A متعامدة.

2. متجهات صفوف A تكون مجموعة عيارية في R" مع الضرب الداخلي الاقليدي.

3. متجهات أعمدة A تكون مجموعة عيارية في R" مع الضرب الداخلي الاقليدي.

البرهان: 1←2

العنصر في الصف i والعمود رقم j في حاصل الضرب AA^T هو الضرب النقطي للمتجه في الصف i من A والمتجه العمود رقم j في A^T. لكن متجه العمود رقم j في A^T هو نفسه متجه الصف رقم j في A. لذا إذا كانت a_n, … , a₂, a₁ هي متجهات صفوف A فإن الضرب AA^T يمكن كتابته بالشكل:

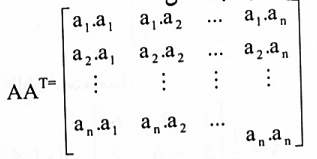
لذا فإن AA^T = 1 إذا وفقط إذا كان 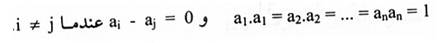،هذه العلاقات تكون صحيحة إذا وفقط إذا {a₁, a₂, …, a_n} مجموعة عيارية في Rⁿ.

بنفس الأسلوب نبرهن 1←3

خواص المصفوفات المتعامدة:

إذا كانت A و B مصفوفتان متعامدتان فإن:

1. معكوس A مصفوفة متعامدة.

2. A B مصفوفة متعامدة.

3 det A = 1   أو  det A = -1

البرهان:

1. بما أن A متعامدة فإن A^T = A^-1 لهذا فإن A^-1 متعامدة.

2. لدينا A^T = A^-1  و  B^T = B^-1  عليه:

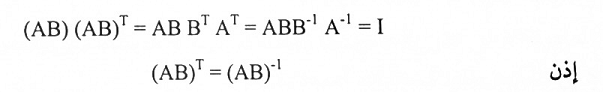
ومن هذا نستنتج ان AB متعامدة.

3. لدينا AA^T = 1

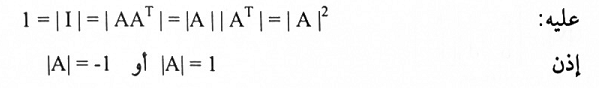
تبديل الأساسات

سنكتفي بشرح طريقة تبديل الأساسات في فضاء البعد الثاني ومن ثم نعمم تلك الطريقة للبعد n.

نفرض v₁, v₂}=S   هي مجموعة الأساس القديم  و v'₁ , v'₂}=S'  الأساس الجديد. لإيجاد مصفوفات الإحداثيات لمتجهات الأساس الجديد نسبة للأساس القديم نفترض أن 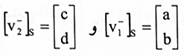أي أن:

ولكي نجد إحداثيات المتجه v القديمة نكتب v بدلالة الأساس S نعوض (2) في (3) سنحصل على:

أي ان مصفوفة الإحداثيات القديمة _s[v] تساوي حاصل ضرب مصفوفة الإحداثيات الجديدة بالمصفوفة 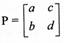 من جهة اليسار حيث أعمدة P هي إحداثيات متجهات الاساس الجديد نسبة للأساس القديم.

وبصورة عامة:

إذا نقلنا أساس فضاء المتجهات V من الأساس القديم v₁, v₂, …, v_n}=S   إلى الأساس الجديد    {v'₁, v'₂, …. , v'_n} S' =  فإن مصفوفة الإحداثيات القديمة _S[v] للمتجه v يمكن ربطها بمصفوفة الإحداثيات الجديدة _s'[v] لنفس المتجه v بواسطة العلاقة:

حيث أن أعمدة P هي مصفوفات إحداثيات الأساس، لجديد نسبة للأساس القديم، أي أن أعمدة P هي:

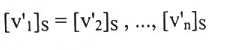
تعريف (1-3):

المصفوفة P التي تنقل الاساس الجديد S' للأساس القديم S تسمى مصفوفة انتقال S' إلى S  ويعبر عنها كمتجهات أعمدة بالشكل:

مثال(3):

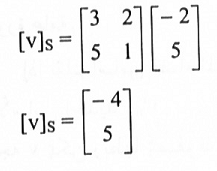
مثال(4):

إذا كانت v'₂, v'₁, v₂, v₁ كما في المثال(3) فما هي مصفوفة الانتقال من S' إلى S. من الواضح أن:

خواص مصفوفات الانتقال:

1. إذا ضربنا مصفوفة الانتقال من S إلى S' بمصفوفة الانتقال من S' إلى S نجد أن:

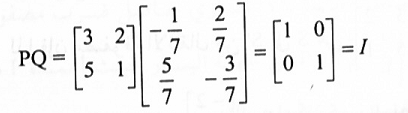
لهذا فإن PQ = 1 أي أن Q = P^-1

2. إذا كانت P مصفوفة الانتقال من S' إلى S. فإن لكل متجه v تتحقق العلاقات الآتية:

3. إذا كانت P مصفوفة انتقال من أساس عياري إلى أساس عياري آخر لفضاء الضرب الداخلي، فإن P مصفوفة متعامدة، أي أن P^-1 = P^T.

مثال(5):

لتكن 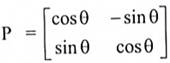  الناتجة من تدوير المحاور y, x بزاوية θ إلى المحاور y' , x'.

عليه فإن:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم المشاريع الهندسية: إنتاج المواد الأوّلية في موقع الصناعات الإنشائية يصل إلى 10 محافظات عراقية

قسم الشؤون الفكرية يفتتح مخيم الرسول الأعظم الكَشفي ويشارك في احتفالية الجالية الإفريقية بالمولد النبوي

متحف الكفيل ينجز 50% من أعمال ترميم مقتنيات العتبة العسكرية المقدسة

المجمَع العلميّ للقرآن الكريم يواصل فعاليات أسبوع ولادة النور القرآني في ديالى

المزيد

الآخبار الصحية

الأطعمة الحارة.. "سر صغير" يغير صحة قلبك وعقلك

وباء صامت.. الملايين حول العالم مصابون بالسكري دون أن يعلموا !

لماذا ينصح بتناول تفاحة يوميا؟

8 فواكه طبيعية تمنحك نوما هنيئا.. وتخلصك من الأرق

المزيد

الآخبار التكنلوجية

ثلاث علامات على وجود مشاكل خطيرة في محرك السيارة ؟

ماذا نعرف عن اللقاح الروسي ضد السرطان؟

مركبة فضاء تعثر على دليل عن وجود حياة قديمة على المريخ

لتدريب الذكاء الاصطناعي.. الصين تخطط لإنشاء شبكة حوسبة موحدة

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام- فضاء المتجهات الحقيقي

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي

أنظمة المعادلات الخطية والمصفوفات -تمارين محلولة