فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
193-205
20-3-2016
19391
الفضاء الاقليدي النوني:
تعريف (1-1):
ليكن n عدداً صحيحاً موجباً . المرتبة فئة n من الأعداد الحقيقية (a1, a2, … , an). مجموعة المرتبات فئة n تسمى الفضاء النوني ويرمز له Rm.
عندما n يساوي 2 أو 3 فإننا نطلق التعبير الزوج المرتب أو الثلاثي المرتب بدلاً من المرتب فئة 2 والمرتب فئة 3. من خلال دراستنا للفصل السابق لاحظنا أن الرمز (a1, a2, a3) له تفسيرات هندسية أما يمثل نقطة أحداثياتها a1 و a2 و a3 أو انه متجه مركباته a1 و a2 و a3 لذا من الممكن اعتبار المرتب فئة n (a1, a2, … , an), على أنه تعميم للنقطة أو تعميم للمتجه (شكل 1-1).
شكل ((1-1
تعريف (1-2):
(1) المتجهان v = (v1, v2, … , vn) و u = (u1, u2, …, un) في "R متساويان، إذا كانت مركباتهما المتناظرة متساوية، أي:
(2) جمع المتجهات v و u، يكتب v + u، هو متجه مركباته عبارة عن جمع مركبات v و u المتناظرة. أي:
(3)ضرب المتجه v بكمية ثابتة k، يكتب kv، هو متجه مركباته هي مركبات v مضروبة في k، أي:
المتجه الصفري في R" يكتب 0 ويعرف (0 = (0, 0, … , 0، إذا كان R"V(v1, v2, …,vn) فإن (-v) هو متجه، يقال له المعكوس الجمعي للمجتهv، ويعرف:
مبرهنة (1-3):
إذا V(v1, v2, …,vn) و u = (u1, u2, …, un) و w = (w1, w2, … , wn) متجهاً في "R.I, k كميات ثابتة، فإن:
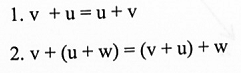
ملاحظة:
بموجب مبرهنة (1-3) يمكن التعامل بالمتجهات من دون استخدام مركباتها، فمثلاً لحل المعادلة x + u = v نضيف النظير –u.
للطرفين:
تعريف (1-4)
لتكن V(v1, v2, …,vn) و u = (u1, u2, …, un) متجهان في R". الضرب الداخلي الاقليدي (الضرب النقطي)، يكتب v.u، يعرف:
مثال(1):
لتكن v = (-1,2,3,1) و u = (0,1,2,4) متجهات في R4 فإن:
مبرهنة (1-5):
لتكن v و u و w في Rn و k ثابت فإن:
البرهان:
نبرهن 2 و 4.
المساواة في الصيغة هذه تكون صحيحة إذا وفقط إذا v1 = v2 = … = 0 إذا وفقط v = 0
تعريف (1-6):
مثال(2): نفرض v = (3,2,1,5) و u = (0,1,-1,3) في R". اوجد طول u والمسافة بينهما.
ملاحظة:
يمكن تمثيل المتجه v = (v1, v2, … , vn)في R" بشكل مصفوفة صف أو مصفوفة عمود:
مثال (3):
مبرهنة (1-7): (متباينة كوجي ــ شفارتز): لتكن v = (v1, v2, … , vn) و u = (u1, u2, …, un)، فإن:
البرهان:
(نبرهن الحالة الخاصة عندما v و u في R2 أما الحالة العامة فسوف نناقشها في المواضيع القادمة).
مبرهنة (1-8):
لتكن v و u متهات في R" و k كمية ثابتة، فإن:
شكل(1-2)
البرهان:
نبرهن الصيغتين (3) و (4)
(4) من شكل (1-2) ( b).
عليه، وبأخذ الجذر التربيعي للطرفين:
بقية الصيغ نبرهن بنفس الطريقة.
مبرهنة (1-9):
لتكن v و u و w في R" ، k كمية ثابتة، فإن:
البرهان ستثبت المتباينة (رقم 4). اما الصيغ الثلاث الأخرى، فتترك كتمارين.
بموجب (2) والمبرهنة (1-8) يكون لدينا:
مبرهنة (1-10):
إذا كانت v و ع متجهات في R". فإن:
البرهان:
لما كان:
تعريف (1-11):
يقال للمجتهدين v و u في R" بأنهما متعامدان إذا:
v.u = 0
مبرهنة (1-12) (فيثاغورس):
إذا تعامد المتجهات v و u في R" فإن
(لأن v و u متعامدان).
مثال(4):
لتكن v و u كما في المثال 3 فإن:
مثال (5):
عليه فإن v و u متعامدان.
مثال(6):
ملاحظة:
الضرب النقطي يساعدنا في تعريف طريقة جديدة لضرب المصفوفات، فمثلاً إذا كانت متجهات صفوف A
هي rn ……, r2,r1 ومتجهات أعمدة B هي cn, … c2, c1 فإن ضرب المصفوفات AB:
عليه ، فالنظام الخطي AX = B يمكن كتابته بصيغة الضرب النقطي:
إذ أن rn, …. , r2, r1 متجهات صفوف A و bn, … b2, b1 عناصر B.
مثال(7)
اكتب النظام الآتي بشكل ضرب نقطي:
الحل:
بموجب الشكل (1-2):
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
