

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
فضاء المتجهات العام- الأساس والبعد
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
257-270
19-3-2016
32132
الأساس والبعد:
مما تقدم نستطيع القول أن الخط المستقيم له بعد واحد والمستوى له بعدين والفضاء من حولنا له ثلاثة أبعاد. في هذا البند سندرس وبشكل أكثر دقة وتفصيلاً بعد فضاء المتجهات.
تعريف (1-1):
لتكن V فضاء متجهات و S = v1,v2,…,vn مجموعة منتهية من متجهات V يقال بأن S هي أساس للفضاء إذا تحققت الشروط الآتية:
1. S مستقلة خطياً.
2. S تنشأ (تكوّن) V.
مثال(1):
نفرض V = R3، مجموعة المتجهات { (0,0,1), (0,1,0), (1,0,0)} S = هي أساس R3 وذلك لأن S مستقل خطياً، كذلك فإن أي متجه في R3 يمكن كتابته:

حيث c, b, a أعداد حقيقية.
لذا فإن S تولد R. عليه فإن S أساس R3، هذا الأساس يسمى الأساس الطبيعي.
مثال(2):
برهن أن  أساس لفضاء المتجهات P2 نبرهن أولاً أن S تنشأ (تكون)P2.
أساس لفضاء المتجهات P2 نبرهن أولاً أن S تنشأ (تكون)P2.
ليكن ax2 + bx + c عنصراً لا على التعيين في P2، نفرض أن


وبحل هذه المعادلات نحصل على c1,= c2 = c3 = 0 أي أن S مستقلة خطياً إذن S هي أساس لفضاء المتجهات P2.
مثال (3):
نفرض أن  لذا فإن S أساس M2x2.
لذا فإن S أساس M2x2.

وهذا يعني أن S تولد M2x2.
مبرهنة (1.2):
لتكن {v1, v2, … , vn} S = أساس لفضاء المتجهات V، فإن كل متجه  يكتب بطريقة واحدة فقط كتركيب خطي من متجهاتS .
يكتب بطريقة واحدة فقط كتركيب خطي من متجهاتS .
البرهان:
نفرض أن v يكتب بطريقتين بالشكل:

سنبرهن أن (i = 1,2, … , n) ai = bi
بطرح المعادلتين نحصل على:

وبما أن S مستقلة خطياً.
عليه فإن a1 – b1 = 0 ومنها a1 = b1 وبنفس الطريقة :

ملاحظة:
إذا كانت {v1, v2, …, vn} S = أساس فضاء المتجهات ولكلv∊V  تسمى إحداثيات v نسبة للأساس S. اما المتجه (c1,c2,…cn)في الفضاء الإقليدي يسمى متجه إحداثيات v نسبة للأساس ويرمز له.
تسمى إحداثيات v نسبة للأساس S. اما المتجه (c1,c2,…cn)في الفضاء الإقليدي يسمى متجه إحداثيات v نسبة للأساس ويرمز له.
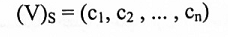
مثال(4):
لاحظنا في المثال 1 أن المتجه v = (a, b, c) في R3 يكتب بالشكل:

حيث {I, j, k} S = هي مجموعة متجهات الأساس الطبيعي، لذا فإن إحداثيات v بالنسبة للأساس الطبيعي في R3 هي c, b, a أي أن:

وبصورة عامة إذا كانت {e1, e2, … , en} S = هي الأساس للفضاء الإقليدي R" حيث:

مثال(5):
اوجد متجه إحداثيات v = (5,-1,9) إذا علمت أن

مثال(6):
ليكن S كما في مثال 5، v∊R2 حيث (V)s=(-1,3,2) أوجد V. بموجب مثال 5 وتعريف (V)s أوجد V. بموجب مثال5 وتعريف (V)s:
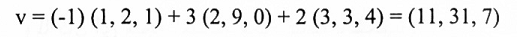
تعريف (1-3):
يقال لفضاء المتجهات غير الصفري V بأنه ذات البعد المنتهي إذا كان يحتوي على مجموعة منتهية من المتجهات {v1,v2,…,vn}تكون أساساً له. إذا لم توجد تلك المجموعة فإن V يقال له فضاء متجهات ذات البعد غير المنتهي.
مثال(7):
فضاء المتجهات في الأمثلة 1 و 2 و 3 ذات البعد المنتهي.
مبرهنة (1-4):
لتكن {v1,v2,…,vn} S = أساس لفضاء المتجهات المنتهي V فإن:
1. أي مجموعة تحتوي على أكثر من n من المتجهات تكون غير مستقلة خطياً.
2. لا توجد مجموعة تحتوي على أقل من n تنشأ (تكون) V.
البرهان:
1. نفرض {v1,v2,…,vm} T = مجموعة من متجهات V، حيث m>n ، بما أن S أساس V فإن أي متجه w1 في V يمكن كتابته كتركيب خطي من متجهات S. أي:

لكي نبرهن أن T غير مستقلة خطياً يجب أن نجد ثوابت km ,…, k2,k1 ليست جميعها أصفار بحيث:

بالتعويض عن wm, ….. w2, w1 نحصل على:
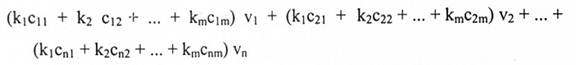
بما أن S مستقلة خطياً فإن برهان T غير مستقلة خطياً يؤول إلى برهان أن الثوابت
km, … , k2, k1 ليست جمعها أصفار والتي تحقق

ولما كان عدد المتغيرات أكثر من عدد المعادلات فإن من الفصل الأول سنحصل على حلولاً ليست صفرية.
برهان2:
لتكن {w1, w2, …, wn} T = مجموعة m من المتجهات في V حيث m<n
نريد أن نبرهن أن T لا تنشأ V. لذا نفرض أن T تنشأ V، عليه فإن أي متجه في V هو تركيب خطي لمتجهات T.
لذا:

وللحصول على التناقض سنبين وجود kn, … , k2, k1 ليست جميعها أصفار بحيث:

وبموجب الفصل الأول فإن هذا النظام الخطي يعطينا حلولاً غير صفرية لأن عدد المتغيرات أكبر من عدد المعادلات.
مبرهنة (1-5):
جميع أساسات فضاء المتجهات ذات البعد المنتهي تحتوي على نفس العدد من المتجهات.
تعريف (1-6):
يعرف بعد فضاء المتجهات V بأنه عدد المتجهات في أساس V، يرمز لها بالرمز dim (v). بعد الفضاء الصفري يساوي صفر.
مثال(8):
في المثال dim R3 = 3,1
في المثال dim p2 = 3,2
في المثال dim M2x2 = 4,3
في المثال dim R" = n, 4
ملاحظة:
الأساس الطبيعي للفضاء الاقليدي Rn يحتوي على n من المتجهات، اما الأساس الطبيعي للفضاء Pn فيحتوي على n + 1 من المتجهات، وأخيراً الأساس الطبيعي للفضاء Mmxn يحتوي على mn من المتجهات.
مبرهنة (1-7):
لتكن S مجموعة غير خالية من المتجهات في فضاء المتجهات V :
1. إذا كانت S مجموعة مستقلة خطياً و v∊V متجه خارج S فإن المجموعة الناتجة من إضافة V إلى S ستبقى مستقلة خطياً.
2. إذا كانS v∊ يمكن التعبير عنه كترتيب خطي لبقية المتجهات في S وإذا حذفنا v من S فإن متجهات S الباقية تنشأ نفس فضاء المتجهات V.
البرهان:
1. نفرض أن {v1, v2, … ,vn} S = مجموعة مستقلة خطياً أيضاً. ولكي نبرهن T مستقلة خطياً فإنه يجب ان تكون

حيث 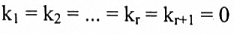 ومن هذا يجب ان تكون
ومن هذا يجب ان تكون  لأن عكس ذلك يعني أن v يمكن كتابته خطي من vr, … , v2, v1 والذي يناقض حقيقة كون v خارج S. لهذا فإن العلاقة 7 يمكن تبسيطها إلى:
لأن عكس ذلك يعني أن v يمكن كتابته خطي من vr, … , v2, v1 والذي يناقض حقيقة كون v خارج S. لهذا فإن العلاقة 7 يمكن تبسيطها إلى:

وبما أن S مجموعة مستقلة خطياً فإن 
2. نفرض أن {v1, v2, …, vr} S = مجموعة من متجهات V. افترض أن أحد متجهات S وليكن Vr تركيب خطي من Vr-1 , ... , v2, v1 . أي

نريد أن نبرهن أنه إذا حذفنا Vr من S فإن المتجهات الباقية  تنشأ نفس الفضاء، بمعنى آخر، يجب أن نبين أنه أي متجه u في Span S يمكن التعبير عنه كتدريب خطي من
تنشأ نفس الفضاء، بمعنى آخر، يجب أن نبين أنه أي متجه u في Span S يمكن التعبير عنه كتدريب خطي من  عليه فإن:
عليه فإن:

ومن العلاقة أعلاه نستنتج أن u يعبر عنها كتركيب خطي من 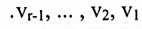
مثال(9):
يمكن وصف المبرهنة (1-7) في الفضاء R3.
1. نفرض S مجموعة متكونة من متجهين مستقلين خطياً في R" تنشأ المستوى خلال نقطة البداية (الشكل 1-1)، إذا أدخلنا متجه إضافي مثل v خارج المستوي، فإن المجموعة الناجمة من ثلاث متجهات ستبقى مستقلة خطياً وذلك لأن أي متجه من المتجهات الثلاث لا يقع في المستوى المتكون من الاثنين الباقيين.

شكل (1-1)
لا يقع أي من المتجهات الثلاث في مستوي الاثنين الباقين
2. نفرض أن S متكونة من ثلاث متجهات غير متطابقة في R3 وتقع جميعها في المستوي المشترك خلال نقط البداية، إذن المتجهات الثلاث تنشأ المستوين. فإذا حذفنا أحد المتجهات من S فإن المجموعة المتبقية المتكونة من متجهين تبقى تنشأ نفس المستوى (لاحظ الشكل 1-2).

شكل (1-2)
يمكن حذف أي متجه مع بقاء المتجهين الباقيين يولدان المستوي بمكن حذف أي من المتجهين المتطابقين مع
بقاء الاثنين الباقيين بولدان المستوي
مبرهنة (1-8):
لتكن V فضاء متجهات ذي البعد n. إذا كانت S هي مجموعة تحتوي بالضبط على n من المتجهات في V، فإن S أساس V إذا كانت S تنشأ V أو S مستقلة خطية.
البرهان:
نفرض أن S تنشأ V. ولكي تكون S أساس V فيجب أن نبرهن أن S مستقلة خطياً. نفرض العكس (أي أن S غير مستقلة خطياً) عليه يوجد v في S هو تركيب خطي من بقية المتجهات، وبحذف هذا المتجه من S وباستخدام مبرهنة (5-4-7) الجزء الثاني. عليه فإن S مستقلة خطياً.
والآن نفرض أن S مستقلة خطياً، ولكي نبرهن أن S اساس V فيجب أن نبين أن S تنشأ V. نفرض العكس (أي S لا تنشأ V). نستنتج من ذلك بأنه يوجد متجه مثل v و V ينتمي إلى S، وبإضافة هذا المتجه فإننا وبوساطة مبرهنة (1-7) نحصل على مجموعة متجهات عددها n + 1 مستقلة خطياً. لكن هذا يناقض مبرهنة (1-4) الجزء الأول، لذا فإن S تنشأ V.
مثال(10):
المتجهين (4,4) و (-1, 3) في R2 تكون أساس للفضاء R2 وذلك لأن أحد المتجهين لا يساوي مضروب الآخر. عليه فإنهما يكونان مجموعة مستقلة خطياً في R2. وبوساطة مبرهنة (1-8) فإنهما يكونان أساس R2.
مثال(11):
المتجهات  تكون أساس للفضاء R3 وذلك لأن u1 و u2 متجهان مستقلان خطياً في المستوى xz- وكذلك المتجه u3 يقع خارج المستوى xz- . لذا فمجموعة المتجهات {u, u2, u3} تكون مستقلة خطياً ولما كان dim R3 = 3 فإن مبرهنة (5-4-8) تعطينا الإجابة وهي أن {u1, u2, u3} أساس R3.
تكون أساس للفضاء R3 وذلك لأن u1 و u2 متجهان مستقلان خطياً في المستوى xz- وكذلك المتجه u3 يقع خارج المستوى xz- . لذا فمجموعة المتجهات {u, u2, u3} تكون مستقلة خطياً ولما كان dim R3 = 3 فإن مبرهنة (5-4-8) تعطينا الإجابة وهي أن {u1, u2, u3} أساس R3.
مبرهنة (1-9):
لتكن S مجموعة منتهية من المتجهات في V ذي البعد n، فإن:
1. إذا كان S مجموعة تنشأ V لكنها ليست أساس إلى V، فإن بالإمكان اختزال S لكي تصبح أساس إلى V من خلال حذف متجهات معينة من S.
2. إذا كانت S مجموعة مستقلة خطياً لكنها ليست أساساً إلى V، فإن بالإمكان توسيع S لكي تصبح أساس بإدخال متجهات معينة إلى S.
البرهان:
1. نفرض أن S مجموعة من المتجهات تنشأ V لكنها ليست أساساً لها. لذا فإن متجه ما في S وليكن u هو تركيب خطي للمتجهات الباقية في S. بوساطة مبرهنة (1-7) يمكن حذف u من S والمجموعة الباقية T ستبقى تنشأ V.
إذا كانت T مستقلة خطياً فإنها ستكون أساس V وهذا هو المطلوب. اما إذا كانت T غير مستقلة خطياً نكرر الخطوة السابعة بحذف متجه ما من T لنحصل على T التي تنشأ V. نستمر في إجراء الطريقة السابقة حتى نحصل على مجموعة من متجهات S ستكون مستقلة خطياً وتنشأ V. المجموعة الجزئية هذه ستكون أساساً إلى V.
2. نفرض dim V = n فإذا كانت S مستقلة خطياً لكنها لا تكون أساساً إلى v وهذا يعني أن S لا تنشأ V، بمعنى آخر، يوجد متجه مثل V في V خارج S. لذا وبوساطة مبرهنة (1-7) يمكننا إضافة v إلى S وتكون النتيجة الحصول على المجموعة T وتكون مستقلة خطياً.
إذا كانت T تكون V، فإن T ستكون أساس V وهذا هو المطلوب. اما إذا كانت T لا تنشأ V، فإننا نضيف متجه ما آخر إلى T للحصول على T' التي تبقى مستقلة خطياً. نستمر بهذه الطريقة بإدخال متجهات معينة حتى نحصل على مجموعة متكونة من n من المتجهات المستقلة خطياً في V، بوساطة مبرهنة (1-7) فإن هذه المجموعة ستكون أساساً للفضاء V.
مثال(12):
لتكن {v1, v2, v3, v4, v5} T = حيث: (v1 = (1,0,1 ، v2 = (0,1,1)، v3 =(0,1,1) ، v4 =(1,2,1) ، v5 = (-1,1,-2) حقق صحة المبرهنة (5-4-9)؟
الحل:
واضح أن T تنشأ V. سنقوم بإيجاد مجموعة جزئية من T بحيث تكون أساساً إلى T.V غير مستقلة خطياً لأن:

ولكن T' غير مستقلة خطياً لأن:

بحذف v3 من T' نحصل على .  والتي تكون V.
والتي تكون V.
وبما أن T' مستقلة خطياً (لماذا؟) عليه فإن T أساس V.
مبرهنة (1-10):
لتكن U فضاء جزئي من V. ذي البعد المنتهي، فإن  . إذا كان dim U = dim V فإن U = V.
. إذا كان dim U = dim V فإن U = V.
البرهان:
نفرض أن {u1, u2, … , um} T = أساس U، لذا فإن T أساس V أو ليس كذلك. فإذا كان T أساس V فإن dim(U) = dim(V) =m وإذا كانت T ليست أساس V فبواسطة مبرهنة (5-4-9) نستطيع إضافة متجهات لمجموعة المتجهات المستقلة خطياً لكي تصبح أساس إلى V. لذا فإن 
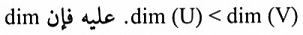 في جميع الحالات.
في جميع الحالات.
إذا كان dim(U) = dim (V) فإن T هي مجموعة متكونة من m من المتجهات المستقلة خطياً في فضاء المتجهات ذي البعد m.
عليه فإن T هي أساس V بموجب (1-8) نستنتج أن U = V
مثال(13):
لتكن W فضاء جزئياً في R3. بموجب مبرهنة (1-10) فإن dim w يمكن أن يكون: صفر، 1،2 او 3 . لذا ستكون لدينا الاحتمالات الآتية:
1. إذا كان dim w = 0 فإن {0}w = أي أن w نقطة.
2. إذا كان dim w = 1 فإن w ستكون مستقيم يمر بنقطة البداية.
3. إذا كان dim w = 2 فإن w ستكون مستوى يمر بنقطة البداية.
4. إذا كان dim w = 3 فإن w ستكون الفضاء R3.
 الاكثر قراءة في الجبر الخطي
الاكثر قراءة في الجبر الخطي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















