

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Voting Systems-The Condorcet Method
المؤلف:
W.D. Wallis
المصدر:
Mathematics in the Real World
الجزء والصفحة:
175-177
16-2-2016
2275
A multiple use of runoff elections was discussed by Marie Jean Antoine Nicolas Caritat, Marquis de Condorcet, an eighteenth Century French mathematician and political theorist. (Similar ideas were proposed by Ramon Llull as long ago as 1299.)
Suppose we simultaneously conduct all the “runoff” elections among our candidates. For example, in the election discussed in Sample Problem 1.2in(Preferential Voting: The Hare Method), there are six runoffs: A versus B, A versus C, A versus D, B versus C, B versus D, and C versus D. If any one candidate wins all his/her runoffs, then surely you would consider that person a winner. We shall call such a candidate a Condorcet winner.
In Sample Problem 1.1in(Sequential Voting), we find:
B beats A 10–9,
A beats C 16–3,
B beats C 12–7,
so B is a Condorcet winner. Similarly, in Sample Problem 1.2in(Preferential Voting: The Hare Method),, D is a Condorcet winner. But even in the simple example
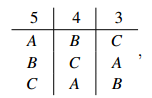
A beats B 8 – 4, B beatsC 9 – 3 andC beats A 7 – 5, so there is no Condorcet winner.
In elections with several candidates, it is very common to have no Condorcet winner, even when there are no ties. This is a serious fault in the Condorcet method.
Condorcet’s own solution to this problem is as follows. We shall construct an ordered list of the candidates. Look at all the runoffs and find out which candidate won with the biggest majority. Looking at Sample Problem 1.1in(Sequential Voting), again, the biggest majority was A beat C 16–3. We’ll denote this A → C. Then look for the secondbiggest, then the third-biggest, and so on, and make a list:
A → C(16−3),B → C(12−7),B → A(10−9).
Now go through this list and construct a preference order of the candidates. At each step, if X → Y, then X precedes Y in the preference list, unless Y already precedes X in the list. In our example, we must have A before C, B before C and B before A.
The list is BAC and clearly B is the winner.
We shall refer to this solution as Condorcet’s extended method, to distinguish it from the case where there is a Condorcet winner under the original method. Note that, if there is a Condorcet winner, the same candidate also wins under the extended method.
Let us apply this to the above example

which has no Condorcet winner. We have, with the larger majorities preceding smaller ones,
B → C(9−3),A → B(8−4),C → A(7−5).
From B → C and A → B we get the list ABC. Next we see C → A, but A already precedes C, so this result is ignored. The final list is ABC, and A is elected, even though a majority of voters would prefer C to A.
Sample Problem 1.1 Consider the election with preference profile:
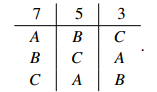
Who would win under the Hare method? Is there a Condorcet winner? Who wins under Condorcet’s solution method?
Solution. The votes for A, B and C are 7, 5 and 3 respectively. Under the Hare method, C is eliminated. The new preference profile is:
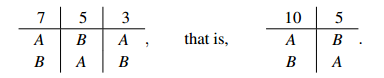
So A wins 10 – 5. Looking at all three runoffs, we see that A beats B 10 – 5, B beats C 12 – 3 and C beats A 8 – 7, so there is no Condorcet winner. For Condorcet’s solution, we see
B → C(12−3),A → B(10−5),C → A(7−5).
The first two yield the list ABC and the last result is ignored, so A is elected.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















