Population Growth
المؤلف:
Steinhaus, H
المصدر:
Mathematical Snapshots, 3rd ed. New York: Dover
الجزء والصفحة:
pp. 290-295
22-12-2021
2610
Population Growth
The differential equation describing exponential growth is
 |
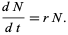(1)
|
This can be integrated directly
 |
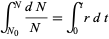(2)
|
to give
 |
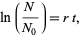(3)
|
where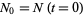 
. Exponentiating,
 |
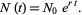(4)
|
This equation is called the law of growth and, in a much more antiquated fashion, the Malthusian equation; the quantity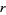 
in this equation is sometimes known as the Malthusian parameter.
Consider a more complicated growth law
 |
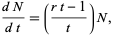(5)
|
where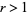 
is a constant. This can also be integrated directly
 |
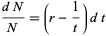(6)
|
 |
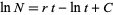(7)
|
 |
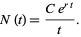(8)
|
Note that this expression blows up at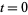 
. We are given the initial condition that 
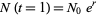, so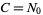 
.
 |
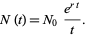(9)
|
The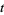 
in the denominator of (◇) greatly suppresses the growth in the long run compared to the simple growth law.
The (continuous) logistic equation, defined by
 |
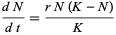(10)
|
is another growth law which frequently arises in biology. It has solution
 |
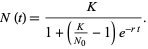(11)
|
REFERENCES:
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 290-295, 1999.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
