For example, suppose we have a system where the messages consist of four binary digits, such as 1100 or 0111. In this example, to send 110011010110, you might first break it up into

                              1100 1101 0110

(so you can send it as three 4-symbol messages). Then each set of 4 digits is replaced by a set of seven digits according to a certain plan. This is called encoding the message. We shall outline one such scheme, where each four-digit string is replaced by a seven-digit string. The three additional digits are calculated using a diagram like a Venn diagram, so the method is called Venn diagram encoding.

We shall represent the original message by the four-digit string ABCD. Each of A, B, C or D represents a 1 or a 0; in the example 1100, A would represent 1, B is 1, C is 0, and D is 0. We transmit a string ABCDEFG.

The set of seven digits is constructed as follows:

First, draw a diagram of three overlapping circles, and write the numbers A, B,  C and D in the positions shown in the left-hand diagram in Fig. 10.1. Then write in three more numbers—E, F, G—chosen as follows. In each circle the sum of the four numbers is to be even.

A + B + C + E must be even.

A + C + D + F must be even.

B + C + D + G must be even.

Fig. 1.1 Venn diagram encoding

Sample Problem 1.1 Encode the message words 1101 and 0110 using Venn diagram encoding.

Solution. Start by forming the following diagrams:

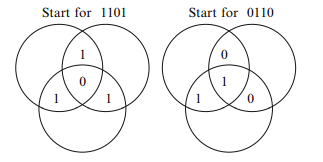
In the diagram for 1101, all three circles contain two 1s, so the sums are all even.

Each of the other three symbols will be 0. In the 0110 diagram, the top left circle is even, so it receives 0 for its new symbol; but each of the others has sum 1,  which is odd, so those circles receive another 1. The final diagrams are

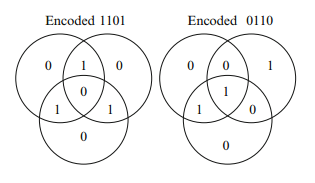
and the strings transmitted will be 1101000 and 0110010 respectively.

The number ABCD is called the message word, and ABCDEFG is called the codeword. This method of constructing codewords from strings of length 4 is called Venn diagram encoding. The person who receives the message fills the numbers into a diagram and checks the three circle sums:

• If they are all even, it is assumed that the correct message was received.

• If any are odd, corrections are made on the assumption that exactly one number is wrong in each odd circle.

This technique has an obvious flaw: if two or more errors are made, the correct message will not be recovered; in fact, the message will be “corrected” to something wrong. But it is reasonably reliable provided the chance of an error is small, and there are other methods available when errors are more likely.

Suppose you receive the codeword 1010010. When you form the diagram, shown on the left of Fig. 1.2, you see that the sum of the top left circle is even (2), but the top right and bottom sums are both odd (3 and 1 respectively). You can change at most one digit, so the only solution is to change the entry common to the two circles, as shown in the right-hand diagram. The corrected codeword is 1011010,  and you believe the intended message was 1011.

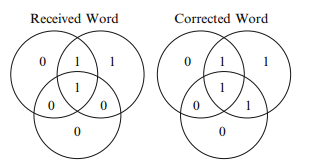
Fig. 1.2 Correcting a codeword with one error

Suppose the sums of the entries in the top left, top right, and bottom circles are X, Y, and Z respectively. Then:

• if only X is odd, change entry E;

• if only Y is odd, change entry F;

• if only Z is odd, change entry G;

• if X and Y are odd, change entry A;

• if X and Z are odd, change entry B;

• if Y and Z are odd, change entry D;

• if all three are odd, change entry C.

And, if all three are even, make no changes.

How useful is this process? Suppose information is being transmitted electronically,  and there is one chance in 10 that an error will be made on any given symbol.

Then the probability of a four-symbol binary message being received correctly is 0.94, or about 0.656. So roughly one in every three messages will be received incorrectly. If there are seven symbols, the chance of no errors is 0.97, approximately 0.478. The chance that the first symbol will be received incorrectly but the rest will be correct is 0.96 × 0.1, and it is the same for each other symbol, so the chance of exactly one error is 0.96 × 0.1 × 7, or 0.372. So the probability of at most one error is 0.85. In those cases the Venn diagram method returns the correct message,  so Venn diagram encoding improves the chance of receiving the message correctly from about 2 in 3 to about 5 in 6.

However, most electrical transmissions are far more reliable than that. If the chance of an error in any symbol is 1 in 100, the probability of an error in a fourdigit transmission is about 1 in 25, while the probability that the message would be decoded correctly using Venn diagram decoding is 0.998—the chance of a mistake in a message is 1 in 500.