من الحقائق التجريبية أنه بالقرب من أي نقطة على سطح الكرة الأرضية، وفي عدم وجود مقاومة للهواء، تسقط جميع الأجسام بنفس العجلة الثابتة. يُسمَّى مقدار هذه العجلة g ويساوي 32 ft/sec² تقريبًا أو meters/sec²  9.8، ويكون اتجاه العجلة لأسفل؛ أي في اتجاه مركز الكرة الأرضية.

مقدار العجلة يتناسب عكسيا مع مربع المسافة من مركز الكرة الأرضية ويكون متجه العجلة في اتجاه مركز الأرض. طبقًا لذلك، يمكن اعتبار مقدار واتجاه العجلة ثابتين فقط في حدود المنطقة التي تكون الأبعاد الخطية فيها صغيرة جدا مقارنة بنصف قطر الكرة الأرضية. هذا ما تعنيه عبارة «بالقرب من».

نؤكد على أنه في غياب مقاومة الهواء لا يعتمد مقدار العجلة واتجاهها على سرعة الجسم (خصوصا إذا قذفت بكرة إلى أعلى تكون العجلة متجهة لأسفل أثناء ارتفاع الكرة، وأثناء سقوطها، وأيضًا عند اللحظة التي تكون فيها عند أعلى نقطة). لا يمكننا في هذه المرحلة من النقاش «استنتاج» حقيقة أن جميع الأجسام تسقط بنفس العجلة لأننا لم نذكر شيئًا عن القوى (وبالأخص القوة التثاقلية) ولا عن كيفية حركة الجسيم استجابة لقوة ما. ومع ذلك، إذا كنا سنتقبل الحقائق التجريبية المعطاة، يمكننا عندئذ استخدام أدواتنا الكينماتيكية للإجابة عن جميع الأسئلة المحتملة عن حركة الجسيم تحت تأثير الجاذبية الأرضية.

ينبغي توجيه المحور بالطريقة الأنسب رياضيا. وسندع المحور y الموجب يشير رأسيًا إلى أعلى (أي خارجًا من مركز الكرة الأرضية). عندئذٍ ينبغي أن يقع المحور x في المستوى الأفقي. نختار اتجاه المحور x بحيث تقع السرعة 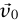 للجسيم عند زمن 0 = t

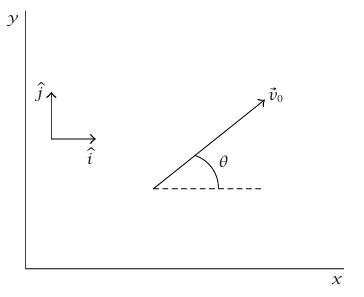
شكل 1–14: متجه السرعة الابتدائية.

في المستوى x–y. وتكون مركبات متجه العجلة هي a_x = a_z = 0, a_y = –g. تؤدي المعادلات ((1–11d)–(1–11a)) الى:

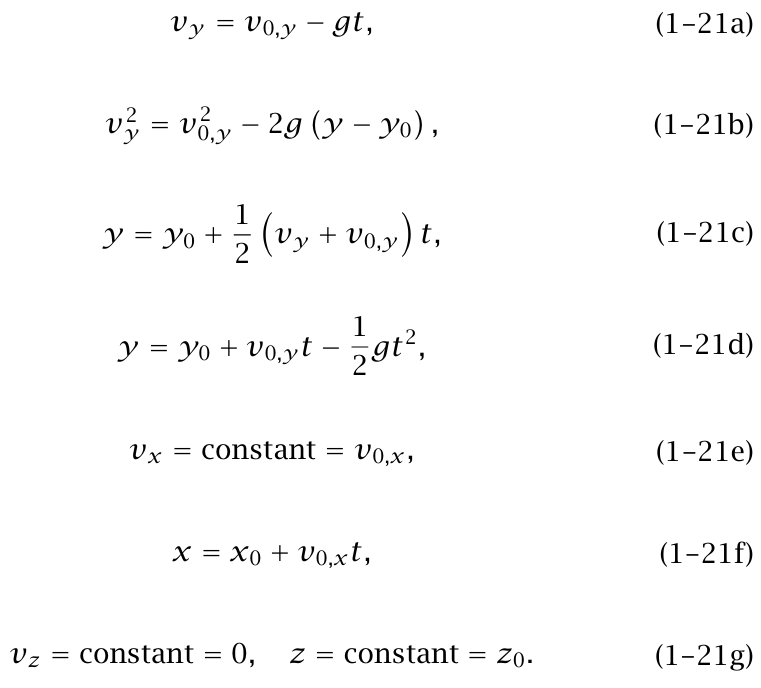
سوف نحدد دائمًا موضع نقطة الأصل بحيث يكون 0 = ₀z، وبذلك تحدث الحركة الكلية في المستوى .x–y عادة ما نضع نقطة الأصل عند الموضع الابتدائي للجسيم بحيث يكون 0 = y₀ =x₀ ، ولكن المعادلات التي في الأعلى لا تفترض هذا.

يمكننا الحصول على معادلة المسار (وهي العلاقة بين y وx) عن طريق حل المعادلة (f 1–21) في t ثم التعويض بالناتج في (d 21–1). نجد أن:

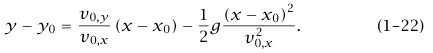
هذه، طبعًا، معادلة قطع مكافئ. إذا وضعنا نقطة الأصل عند الموضع الابتدائي للجسيم، وإذا حددنا مقدار السرعة الابتدائية ₀v والزاوية θ بين السرعة الابتدائية والمحور x (وبالتالي يكون v₀y = v₀ sinθ , v₀x = v₀ cosθ)، عندئذ تكون معادلة المسار هي:

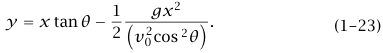
إذا تم إطلاق مدفع من نقطة على سطح الأرض، فإن المدى الأفقي R يُعَرَّف بأنه المسافة من نقطة الإطلاق إلى المكان الذي ترتطم عنده القذيفة بسطح الأرض. إذا وضعنا 0 = y في المعادلة (23–1) نجد أن:

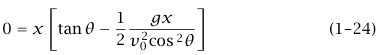
هذه المعادلة لها جذران،  الجذر الأول هو، طبعًا، نقطة الإطلاق، والجذر الثاني يخبرنا بالمكان الذي هبطت عنده القذيفة؛ أي:

إذا أردنا زيادة المدى لمقدار معين من سرعة إطلاق فوهة المدفع v₀ إلى الحد الأقصى، فينبغي لنا الإطلاق بالزاوية التي تجعل من (2θ) sin قيمة عظمى؛ أي       °45 = θ.

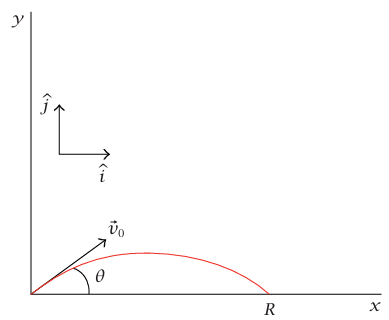
شكل 1–15: مسار قطع مكافئ.

أبسط طريقة لإيجاد أقصى ارتفاع تصل إليه قذيفة ما هو استخدام المعادلة (b 21–1)، يمكننا أيضًا وضع dy/dx=0 وإيجاد 2/x = R ، وهو الأمر البدهي عندما تأخذ في الاعتبار تماثل القطع المكافئ. عندها يمكننا تقدير لا عندما يكون 2/x = R.