المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | زوايا متحالفة Allied Angles |
 49286
 01:47 صباحاً
التاريخ: 13-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 157|
أقرأ أيضاً
التاريخ: 9-2-2017
1127
التاريخ: 12-2-2017
1135
التاريخ: 13-2-2017
1368
التاريخ: 13-2-2017
4350
|
الزاويتان المتحالفتان هما الزاويتان الداخليتان وتقعان داخل المستقيمين ل1 , ل2 وعلى جهة واحدة كما في الشكل .
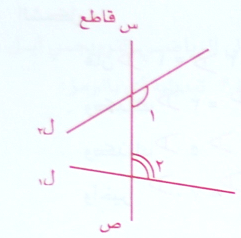
من القاطع س , ص حيث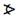 
1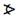 , 2 متحالفتان .
وإذا كان المستقيمان ل1 , ل2 متوازيين كما في الشكل .
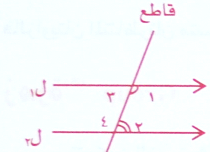
فإن 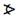1 + 4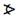=180○ بالتحالف
وكذلك 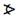3 + 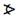4=180○ بالتحالف
وللتوضيح فإن الزاويتين المتحالفتان تشكلان حرف 
فالزاويتان المتحالفتان متكاملتان بالقياس إذا كان ل1 , ل2 متوازيان .
|
|
|
|
أكبر مسؤول طبي بريطاني: لهذا السبب يعيش الأطفال حياة أقصر
|
|
|
|
|
|
|
طريقة مبتكرة لمكافحة الفيروسات المهددة للبشرية
|
|
|
|
|
|
|
جامعة الكفيل تناقش تحضيراتها لإطلاق مؤتمرها العلمي الدولي السادس
|
|
|
