
The efficiency of an ideal engine
 المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
 المصدر:
The Feynman Lectures on Physics
المصدر:
The Feynman Lectures on Physics
 الجزء والصفحة:
Volume I, Chapter 44
الجزء والصفحة:
Volume I, Chapter 44
 2024-06-08
2024-06-08
 1757
1757
Now we shall try to find the law which determines the work W as a function of Q1, T1, and T2. It is clear that W is proportional to Q1, for if we consider two reversible engines in parallel, both working together and both double engines, the combination is also a reversible engine. If each one absorbed heat Q1, the two together absorb 2Q1 and the work done is 2W, and so on. So it is not unreasonable that W is proportional to Q1.
Now the next important step is to find this universal law. We can, and will, do so by studying a reversible engine with the one particular substance whose laws we know, a perfect gas. It is also possible to obtain the rule by a purely logical argument, using no particular substance at all. This is one of the very beautiful pieces of reasoning in physics and we are reluctant not to show it to you, so for those who would like to see it we shall discuss it in just a moment. But first we shall use the much less abstract and simpler method of direct calculation for a perfect gas.
We need only obtain formulas for Q1 and Q2 (for W is just Q1−Q2), the heats exchanged with the reservoirs during the isothermal expansion or contraction. For example, how much heat Q1 is absorbed from the reservoir at temperature T1 during the isothermal expansion [marked (1) in Fig. 44–6] from point a, at pressure pa, volume Va, temperature T1, to point b with pressure pb, volume Vb, and the same temperature T1? For a perfect gas each molecule has an energy that depends only on the temperature, and since the temperature and the number of molecules are the same at a and at b, the internal energy is the same. There is no change in U; all the work done by the gas,

during the expansion is energy Q1 taken from the reservoir. During the expansion, pV=NkT1, or

is the heat taken from the reservoir at T1. In the same way, for the compression at T2 [curve (3) of Fig. 44–6] the heat delivered to the reservoir at T2 is

To finish our analysis we need only find a relation between Vc/Vd and Vb/Va. This we do by noting that (2) is an adiabatic expansion from b to c, during which pVγ is a constant. Since pV=NkT, we can write this as (pV)Vγ−1=const or, in terms of T and V, as TVγ−1=const, or

Likewise, since (4), the compression from d to a, is also adiabatic, we find

If we divide this equation by the previous one, we find that Vb/Va must equal Vc/Vd, so the ln’s in (44.4) and (44.5) are equal, and that

This is the relation we were seeking. Although proved for a perfect gas engine, we know it must be true for any reversible engine at all.
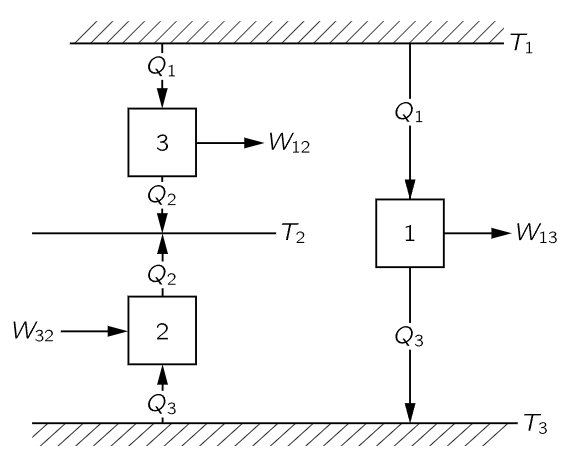
Fig. 44–8. Engines 1 and 2 together are equivalent to engine 3.
Now we shall see how this universal law could also be obtained by logical argument, without knowing the properties of any specific substances, as follows. Suppose that we have three engines and three temperatures, let us say T1, T2, and T3. Let one engine absorb heat Q1 from the temperature T1 and do a certain amount of work W13, and let it deliver heat Q3 to the temperature T3 (Fig. 44–8). Let another engine run backwards between T2 and T3. Suppose that we let the second engine be of such a size that it will absorb the same heat Q3, and deliver the heat Q2. We will have to put a certain amount of work, W32, into it—negative because the engine is running backwards. When the first machine goes through a cycle, it absorbs heat Q1 and delivers Q3 at the temperature T3; then the second machine takes the same heat Q3 out of the reservoir at the temperature T3 and delivers it into the reservoir at temperature T2. Therefore the net result of the two machines in tandem is to take the heat Q1 from T1, and deliver Q2 at T2. The two machines are thus equivalent to a third one, which absorbs Q1 at T1, does work W12, and delivers heat Q2 at T2, because W12=W13−W32, as one can immediately show from the first law, as follows:
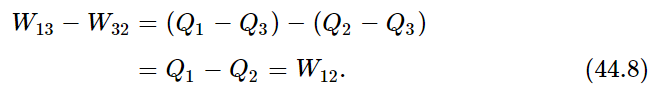
We can now obtain the laws which relate the efficiencies of the engines, because there clearly must be some kind of relationship between the efficiencies of engines running between the temperatures T1 and T3, and between T2 and T3, and between T1 and T2.
We can make the argument very clear in the following way: We have just seen that we can always relate the heat absorbed at T1 to the heat delivered at T2 by finding the heat delivered at some other temperature T3. Therefore, we can get all the engines’ properties if we introduce a standard temperature, analyzing everything with that standard temperature. In other words, if we knew the efficiency of an engine running between a certain temperature T and a certain arbitrary standard temperature, then we could work out the efficiency for any other difference in temperature. Because we assume we are using only reversible engines, we can work from the initial temperature down to the standard temperature and back up to the final temperature again. We shall define the standard temperature arbitrarily as one degree. We shall also adopt a special symbol for the heat which is delivered at this standard temperature: we shall call it QS. In other words, when a reversible engine absorbs the heat Q at temperature T, it will deliver, at the unit temperature, a heat QS. If one engine, absorbing heat Q1 at T1, delivers the heat QS at one degree, and if an engine absorbing heat Q2 at temperature T2 will also deliver the same heat QS at one degree, then it follows that an engine which absorbs heat Q1 at the temperature T1 will deliver heat Q2 if it runs between T1 and T2, as we have already proved by considering engines running between three temperatures. So all we really have to do is to find how much heat Q1 we need to put in at the temperature T1 in order to deliver a certain amount of heat QS at the unit temperature. If we discover that, we have everything. The heat Q, of course, is a function of the temperature T. It is easy to see that the heat must increase as the temperature increases, for we know that it takes work to run an engine backwards and deliver heat at a higher temperature. It is also easy to see that the heat Q1 must be proportional to QS. So the great law is something like this: for a given amount of heat QS delivered at one degree from an engine running at temperature T degrees, the heat Q absorbed must be that amount QS times some increasing function of the temperature:

 الاكثر قراءة في الديناميكا الحرارية
الاكثر قراءة في الديناميكا الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


