
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
توزيع بولتزمان
المؤلف:
بيتر أتكينز
المصدر:
الكيمياء الفيزيائية
الجزء والصفحة:
ص 46 – ص 49
2024-10-01
1709
ثمة استنتاج استثنائي واحد من الديناميكا الحرارية الإحصائية يمثل بلا أدنى شك أهمية كبيرة بالنسبة إلى الكيمياء الفيزيائية ويفسر التنويعات الشاسعة لخواص المادة، وفي ذلك تفاعلاتها الكيميائية ويلقي الضوء على الخاصية المحيرة المتمثلة في درجة الحرارة.
إحدى النتائج المترتبة على ميكانيكا الكم هي أن الذرة أو الجزيء يمكن أن توجد في حالات معينة من الطاقة فقط؛ أي إن طاقتها يعبر عنها «كميا» ولا يمكن أن تتغير باستمرار حسب الرغبة. فعند درجة حرارة الصفر المطلق، تكون جميع الجزيئات في أدنى حالات الطاقة الخاصة بها، أي في الحالة القاعدية الخاصة بها. وعندما ترتفع درجة الحرارة، تهرب بعض الجزيئات من الحالة القاعدية ونجدها في حالات طاقة أعلى. وعند أي درجة حرارة أعلى من الصفر المطلق، مثل درجة حرارة الغرفة، تنتشر الجزيئات في جميع حالاتها المتاحة، مع وجود معظمها في الحالة القاعدية وعدد أقل تدريجيا في حالات الطاقة المتزايدة.
التوزيع متغير باستمرار نظرًا إلى أن الجزيئات تتبادل الطاقة، ربما عبر التصادمات في أحد الغازات، عندما ينطلق جزيء ما في تصادمه بسرعة عالية ويصل الجزيء الآخر إلى نقطة توقف تقريبًا. ومن المستحيل في ضوء وجود تريليونات الجزيئات في العينة النموذجية، تتبع التوزيع المتغير. ومع ذلك، تبين أنه في مثل هذه العينات النموذجية ثمة توزيع واحد محتمل أكثر على نحو كبير ويمكن تجاهل جميع التوزيعات الأخرى، وهذا التوزيع السائد هو «توزيع بولتزمان».
سأجعل هذا الوصف مرئيا أكثر بعض الشيء. لنفترض أن لديك مجموعة من أرفف الكتب، كل رف منها يمثل مستوى للطاقة، وأنت ترص الكتب على الأرفف بعشوائية. يمكنك أن تتخيل أنه في إحدى المحاولات وصلت إلى توزيع معين للكتب، ربما توزيع بعدد متساوٍ على كل رف. من الممكن تحقيق ذلك التوزيع إلا أن هذا الاحتمال مستبعد جدًّا. وفي محاولة أخرى، يستقر نصف عدد الكتب على أدنى رف والنصف الآخر على أعلى رف. هذا أيضًا أمر غير مرجح؛ إلا أنه أكثر احتمالاً من التوزيع الأول. (في الواقع، إذا كان لديك 100 كتاب و10 أرفف، فستكون احتمالية هذا أكثر بنحو 1063 × 2 مرة!) وعندما تواصل تكديس الكتب مع ملاحظة التوزيع مع كل محاولة ستحصل عادة على توزيعات مختلفة في كل مرة. ومع ذلك، سيظهر توزيع واحد مرة تلو الأخرى وهذا التوزيع الأكثر احتمالا هو توزيع بولتزمان.
تعليق
حتى لا تزداد هذه المناقشة تعقيدًا، سأتغاضى عن جانب مهم، ألا وهو أن كل توزيع ربما تناظره طاقة إجمالية مختلفة؛ يجب التخلص من أي توزيع لا يناظر الطاقة الفعلية للنظام. ولذا، على سبيل المثال، ما لم تكن درجة الحرارة صفرًا، فإننا نستبعد التوزيع الذي توجد فيه جميع الكتب على أدنى رف. ويُستبعد أيضًا توزيع الكتب على أعلى رف وعلماء الكيمياء الفيزيائية يعرفون كيف يقومون بذلك على أكمل وجه.
سمي توزيع بولتزمان على اسم العالم لودفيج بولتزمان (1844–1906)، المؤسس الرئيسي لعلم الديناميكا الحرارية الإحصائية. ولهذا التوزيع صيغة بسيطة جدًّا من الناحية الرياضية: إنها دالة تضاؤل أسي للطاقة (أحد التعبيرات عن تلك الصيغة هو كما يلي: e–E/kT، حيث إن E يرمز للطاقة، وT يرمز لدرجة الحرارة المطلقة، و يرمز للثابت الأساسي الذي نسميه الآن بثابت بولتزمان). وهذا يعني أن احتمالية العثور على جزيء في حالة طاقة معينة تتضاءل سريعًا مع زيادة الطاقة؛ لذا سيُعثر على أغلب الجزيئات في حالات طاقة متدنية وعدد قليل جدًّا سيُعثر عليه في حالات طاقة عالية.
تعليق
إن توزيع بولتزمان غاية في الأهمية والبساطة في آن واحد لدرجة أنه ينبغي أن أوضح أحد أشكال صيغه. إذا كانت الحالتان تحظيان بطاقتين E1 وE2، فعند درجة حرارة T، تكون نسبة أعداد الجزيئات في هاتين الحالتين كما يلي: N2/N1 = e – (E2–E1)/kT
يتوقف الوصول إلى طرف دالة التضاؤل الأسي، أو في الواقع شكلها العام، على معامل واحد موجود في التعبير؛ ألا وهو: درجة الحرارة T انظر شكل (3–1). فإذا كانت درجة الحرارة منخفضة، فإن التوزيع ينخفض بسرعة بالغة لدرجة أن أدنى المستويات فقط يجري شغلها على نحو ملحوظ . وإذا كانت درجة الحرارة عالية، يتراجع التوزيع ببطء شديد مع زيادة الطاقة، ويجري شغل الكثير من حالات الطاقة العالية. وإذا كانت درجة الحرارة صفرًا، فإن توزيع جميع الجزيئات سيكون في الحالة القاعدية. وإذا كانت درجة الحرارة عالية على نحو لا نهائي، تشغل الجزيئات جميع الحالات المتاحة على نحو متساو. وهذا هو تفسير درجة الحرارة الذي ذكرته : إنها المعامل العام الوحيد الذي يحدد التوزيع الأكثر احتمالًا للجزيئات عبر الحالات المتاحة. وهذا الفهم أيضًا يعد خطوة أساسية في فهم الميكانيكا الحرارية من منظور بولتزمان، نظرًا إلى أن درجة الحرارة هي المعامل الذي قدمه القانون الصفري. وسنلاحظ فيما يلي إلى أي مدى أوضحت الرؤية الثاقبة لبولتزمان أيضًا الأساس الجزيئي للقانون الأول والثاني والثالث للديناميكا الحرارية.
يصف توزيع بولتزمان جانبين من جوانب الكيمياء الاستقرار والتفاعلية. فعند درجات الحرارة العادية، يشير التوزيع ضمنًا إلى أن معظم الجزيئات تكون في حالات متدنية من الطاقة. وذلك يناظر حالة الاستقرار، ونحن محاطون بالجزيئات والمواد الصلبة التي تبقى لفترات طويلة. ومن ناحية أخرى، توجد بعض الجزيئات في حالات طاقة عالية، لا سيما في درجة الحرارة العالية، وهذه هي الجزيئات التي تخضع للتفاعلات. وعلى الفور نستطيع أن نفطن إلى سبب حدوث معظم التفاعلات الكيميائية بسرعة أكبر في ظل درجات حرارة عالية. يمكن اعتبار الطهي، مثلا، عملية يصل فيها توزيع بولتزمان إلى مستويات طاقة أعلى من خلال رفع درجات الحرارة، ويرتقي عدد أكبر من الجزيئات إلى حالات طاقة أعلى، وبالتالي تكون قادرة على الخضوع للتغير إن بولتزمان، رغم ضيق رؤيته، أمعن النظر أكثر إلى داخل المادة مقارنةً بمعظم معاصريه.
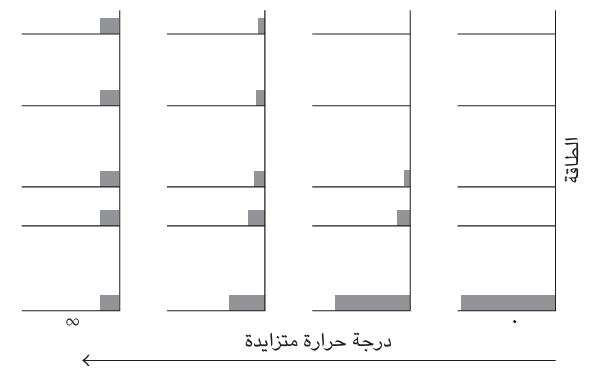
شكل 3–1: توزیع بولتزمان لسلسلة من درجات الحرارة. تصف الخطوط الأفقية الطاقات المسموح بها للنظام وتمثل المستطيلات المظللة الأعداد النسبية للجزيئات في كل مستوى عند درجة الحرارة المذكورة.
 الاكثر قراءة في الديناميكا الحرارية
الاكثر قراءة في الديناميكا الحرارية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















