


 Grammar
Grammar
 Tenses
Tenses
 Present
Present
 Past
Past
 Future
Future
 Parts Of Speech
Parts Of Speech
 Nouns
Nouns
 Verbs
Verbs
 Adverbs
Adverbs
 Adjectives
Adjectives
 Pronouns
Pronouns
 Pre Position
Pre Position
 Preposition by function
Preposition by function 
 Preposition by construction
Preposition by construction
 Conjunctions
Conjunctions
 Interjections
Interjections
 Grammar Rules
Grammar Rules
 Linguistics
Linguistics
 Semantics
Semantics
 Pragmatics
Pragmatics
 Reading Comprehension
Reading Comprehension|
Read More
Date: 1-2-2022
Date: 25-1-2023
Date: 2-2-2022
|
We have used a system of category labels based on the bar notation which has been widely adopted since the 1970s. Within this framework, a sentence like (the title of Gloria Gaynor’s immortal song) I will survive has the structure (66) below:

The bar notation used in (66) posits that there are three different levels of projection (i.e. types of expression): (i) heads (also called minimal projections) like the T/tense auxiliary will; (ii) intermediate projections like the T-bar will survive; and (iii) maximal projections like the TP I will survive. However, Chomsky (1999, p. 2) argues that a system of category labels which posits three different types of category label for projections of a given head H (viz. H, H-bar and HP) violates a UG principle which he terms the Inclusiveness Condition – outlined informally below:
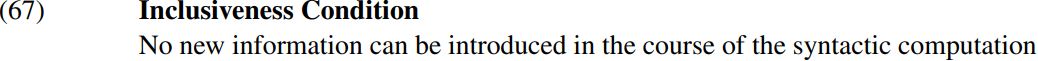 The reason why the bar notation used in trees like (66) violates inclusiveness is as follows. When the word will is taken out of the lexicon, its lexical entry specifies that it has a set of properties which include the grammatical properties represented by the category label T in (66). But the tree in (66) tells us that when will is merged with its complement survive, the resulting string will survive belongs to the category T-bar – in other words, it is an intermediate projection of will. Likewise, the tree in (66) also tells us that the larger string I will survive is a TP – in other words, it is the maximal projection of will. But this information about intermediate and maximal projections is not part of the lexical entry for will, and hence must be added in the course of the syntactic computation. However, adding such information about projection levels violates the Inclusiveness Condition (67).
The reason why the bar notation used in trees like (66) violates inclusiveness is as follows. When the word will is taken out of the lexicon, its lexical entry specifies that it has a set of properties which include the grammatical properties represented by the category label T in (66). But the tree in (66) tells us that when will is merged with its complement survive, the resulting string will survive belongs to the category T-bar – in other words, it is an intermediate projection of will. Likewise, the tree in (66) also tells us that the larger string I will survive is a TP – in other words, it is the maximal projection of will. But this information about intermediate and maximal projections is not part of the lexical entry for will, and hence must be added in the course of the syntactic computation. However, adding such information about projection levels violates the Inclusiveness Condition (67).
One way of avoiding violation of inclusiveness is to remove all information about projection levels from trees, and hence replace a tree like (66) above by one like (68) below:
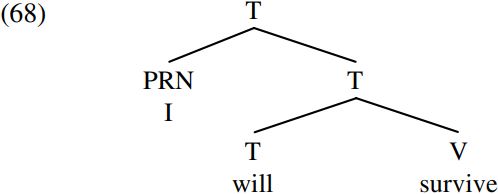
What our revised tree (68) says is that will, will survive and I will survive are all projections of the tense auxiliary will and hence are all tense expressions. Moreover, information about projection levels turns out to be entirely redundant, since it is predictable from looking at the relative positions of constituents within a given structure. Simply by looking at the positions they occupy in the tree (68) we can tell that will is the minimal projection of will (i.e. it is the smallest expression headed by will), that will survive is an intermediate projection of will (by virtue of being neither the smallest nor the largest expression headed by will) and that I will survive is the maximal projection of will (by virtue of being the largest expression headed by will). Similarly, we can tell that the V survive is both a minimal and a maximal projection, in that it is both the smallest and the largest expression headed by survive: hence (e.g.) it can behave like a maximal projection and undergo preposing (as in Survive, I will). In much the same way, we know from looking at the structure in (68) that the pronoun I is likewise both a minimal and a maximal projection: given their status as maximal projections, it follows that pronouns can undergo preposing (as with the pronoun him in Him, I would never trust). Since the information about projection levels in the bar notation is redundant, Chomsky reasons, such information should not be represented in the system of category labels used in tree diagrams: after all, the goal of Minimalism is to reduce theoretical apparatus to the minimum which is conceptually necessary.
Given the possibility (mentioned in §2.11) that categorial information (i.e. information about the category that an item belongs to) can be represented in terms of grammatical features (and hence subsumed within the set of features which characterize the idiosyncratic properties of individual words), a further possibility is that category labels like those in (68) can be entirely replaced by sets of features, so opening up the possibility of developing a theory of bare phrase structure – i.e. a theory in which there are no category labels in syntactic trees. An even more radical possibility along these lines would be for the structure of I will survive to be represented in terms of an unlabeled tree diagram like (69) below:
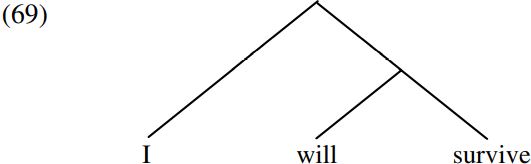
An unlabeled tree diagram like (69) tells us that the constituents of (69) are I, will, survive, will survive and I will survive. The lexical entries for the items I, will and survive comprise sets of features which include information about their grammatical and selectional properties: for example, the entry for will tells us that it is a finite auxiliary which selects an infinitival complement. The fact that will selects an infinitive complement (and that survive is an infinitive form and is the sister of will) means that survive must be the complement of will and hence that will survive is a projection of will. Likewise, the fact that will has an [EPP] feature requiring it to project a subject means that the nominative pronoun I must be the subject of will, and hence that I will survive is an extended projection of will. As before, the relative position of the relevant constituents within the overall structure tells us that will is a minimal projection (of itself), will survive is an intermediate projection of will, and I will survive is the maximal projection of will. The overall conclusion we arrive at is that the information about category labels and projection levels in a conventional labelled tree diagram like (66) above may well be redundant.
If the kind of reasoning outlined here is along the right lines, it opens up the possibility of developing a theory of bare phrase structure such as that outlined in a skeletal form in Chomsky (1995) and Uriagereka (1998) – though it should be noted that the relevant discussion in these two works is highly technical and not suitable for those who don’t have some mathematical background in set theory. However, we shall continue to use traditional labelled trees and the bar notation to represent structure, category membership and projection levels throughout the rest of this topic, since this remains the notation most widely used in contemporary work in syntax.
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|