


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 30-1-2022
التاريخ: 26-1-2022
التاريخ: 22-2-2022
التاريخ: 29-1-2022
|
تعريف مفردات البرمجة الخطية
1- التغيرات (Variables)
يقصد بالمتغير الذي يرمز له بقيمة مثل (n........... xi (j= 1,2,3,
2- المغفور للتحكم فيه (Continuous variable)
هو متغير تحت تصرف من يتخذ القرار.
3- التغير المستمر (Continuous variable)
هو متغير ذو قيمة محصورة بين حدود عظمى ودنيا.
4- العام الشماع (Discrete variable)
هو المتغير الذي يأخذ قيم موصوفة بدرجات معلومات
مثال X لا يمكن أن تأخذ القيم 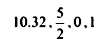
5- المقابر المقطع (Linear Function)
هي الدوال أو المعادلات التي لا تأخذ في أسها إلا واحد فقط.
مثال x + x وليس X1 log x2 . وتعتبر هذه الدوال من ذات المتغير المستمر
6- الدوال في الخطية (Non liner Function):
عكس الدوال الخطية ويمكن أن يكون أسها أقل و أكثر من (1).
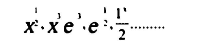
وتعتبر هذه الدوال من الدوال ذات المتغير المتقطع.
7- النمط الرياضي (Mathematical model)
هو نمط يحدد العلاقة بين متغيرات وثابت تحاكي واقع أي نظام، والنمط الرياضي الخطي هو الذي يحوي على معادلات خطية فقط.
8- المعادلات (Equations)
ويمكن تمثيلها بواسطة الآتي:
F(x) = b
ويعني هذا أن بعض الدوال تحتوي على متغيرات في الطرف الشمالي.
X = X1 , X2 X3 ……....... Xn
وعلى طرف يمين يساوي (b)
9- الغير متعادلات (Inequalities)
ويقصد بها المعادلات التي طرفها الشمالي لا يساوي الطرف الأيمن فقط، بل يزيد أو يقل عنه. ويمكن التعبير عنها رياضياً على النحو التالي:
f(x) ≤ b
f(x) > b
10- الأهداف (Objectives)
ويمكن تمثيلها رياضياً بواسطة المعادلة التالية:
Minimize f(x) or maximize f(x)
وهو تعبير عن تصغير التكاليف أو المسافات أو تعظيم الربح أو الإنتاج.
11- القيود (Constraints)
هي عبارة عن معادلات يجب أن تحقق رياضياً في ظل الهدف، ويمكن أن يعبر عنها رياضياً.
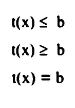
ويعتمد على حالة الإنتاجية.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|