Löwenheim-Skolem Theorem

The Löwenheim-Skolem theorem is a fundamental result in model theory which states that if a countable theory has a model, then it has a countable model. Furthermore, it has a model of every cardinal number greater than or equal to 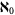 (aleph-0). This theorem established the existence of "nonstandard" models of arithmetic.

The Löwenheim-Skolem theorem establishes that any satisfiable formula of first-order logic is satisfiable in an 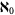 (aleph-0) domain of interpretation. Hence, aleph-0 domains are sufficient for interpretation of first-order logic.

REFERENCES:

Berry, G. D. W. Symposium on the Ontological Significance of the Löwenheim-Skolem Theorem, Academic Freedom, Logic, and Religion. Philadelphia, PA: Amer. Philos. Soc., pp. 39-55, 1953.

Beth, E. W. "A Topological Proof of the Theorem of Löwenheim-Skolem-Gödel." Nederl. Akad. Wetensch., Ser. A 54, 436-444, 1951.

Beth, E. W. "Some Consequences of the Theorem of Löwenheim-Skolem-Gödel-Malcev." Nederl. Akad. Wetensch., Ser. A 56, 66-71, 1953.

Chang, C. C. and Keisler, H. J. Model Theory, 3rd enl. ed. New York: Elsevier, 1990.

Church, A. §45 and 49 in Introduction to Mathematical Logic. Princeton, NJ: Princeton University Press, 1996.

Curry, H. B. Foundations of Mathematical Logic, 2nd rev. ed. New York: Dover, pp. 6-7, 95-96, and 121, 1977.

Fraenkel, A. A. and Bar-Hillel, Y. Foundations of Set Theory. Amsterdam, Netherlands, p. 105, 1958.

Myhill, J. Symposium on the Ontological Significance of the Löwenheim-Skolem Theorem, Academic Freedom, Logic, and Religion. Philadelphia, PA: Amer. Philos. Soc., pp. 57-70, 1953.

Quine, W. V. "Completeness of Quantification Theory: Löwenheim's Theorem." Appendix to Methods of Logic, rev. ed. New York: pp. 253-260, 1959.

Quine, W. V. "Interpretation of Sets of Conditions." J. Symb. Logic 19, 97-102, 1954.

Rasiowa, H. and Sikorski, R. "A Proof of the Löwenheim-Skolem Theorem." Fund. Math. 38, 230-232, 1952.

Skolem, T. "Sur la portée du théorème de Löwenheim-Skolem." Les Entretiens de Zurich sur les fondements et la méthode des sciences mathématiques (December 6-9, 1938), pp. 25-52, 1941.

Vaught, R. L. "Applications of the Löwenheim-Skolem-Tarski Theorem to Problems of Completeness and Decidability." Nederl. Akad. Wetensch., Ser. A 57, 467-472, 1954.