


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-2-2017
Date: 27-12-2021
Date: 29-12-2021
|
Let 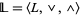 and
and 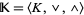 be lattices, and let
be lattices, and let 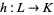 . Then
. Then 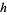 is a lattice homomorphism if and only if for any
is a lattice homomorphism if and only if for any 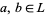 ,
, 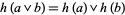 and
and 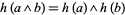 . Thus a lattice homomorphism is a specific kind of structure homomorphism. In other words, the mapping
. Thus a lattice homomorphism is a specific kind of structure homomorphism. In other words, the mapping 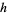 is a lattice homomorphism if it is both a join-homomorphism and a meet-homomorphism.
is a lattice homomorphism if it is both a join-homomorphism and a meet-homomorphism.
If 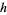 is a one-to-one lattice homomorphism, then it is a lattice embedding, and if a lattice embedding is onto, then it is a lattice isomorphism.
is a one-to-one lattice homomorphism, then it is a lattice embedding, and if a lattice embedding is onto, then it is a lattice isomorphism.
An example of an important lattice isomorphism in universal algebra is the isomorphism that is guaranteed by the correspondence theorem, which states that if 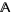 is an algebra and
is an algebra and 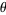 is a congruence on
is a congruence on 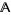 , then the mapping
, then the mapping ![h:[theta,del _A]->Con(A/theta)](https://mathworld.wolfram.com/images/equations/LatticeHomomorphism/Inline13.gif) that is defined by the formula
that is defined by the formula
![h(phi)=phi/theta={([a]_theta,[b]_theta) in (A/theta)^2|(a,b) in phi}](https://mathworld.wolfram.com/images/equations/LatticeHomomorphism/NumberedEquation1.gif) |
is a lattice isomorphism.
REFERENCES:
Bandelt, H. H. "Tolerance Relations on Lattices." Bull. Austral. Math. Soc. 23, 367-381, 1981.
Birkhoff, G. Lattice Theory, 3rd ed. Providence, RI: Amer. Math. Soc., 1967.
Burris, S. and Sankappanavar, H. P. A Course in Universal Algebra. New York: Springer-Verlag, 1981. http://www.thoralf.uwaterloo.ca/htdocs/ualg.html.
Chajda, I. and Zelinka, B. "Tolerances and Convexity." Czech. Math. J. 29, 584-587, 1979.
Chajda, I. and Zelinka, B. "A Characterization of Tolerance-Distributive Tree Semilattices." Czech. Math. J. 37, 175-180, 1987.
Gehrke, M.; Kaiser, K.; and Insall, M. "Some Nonstandard Methods Applied to Distributive Lattices." Zeitschrifte für Mathematische Logik und Grundlagen der Mathematik 36, 123-131, 1990.
Grätzer, G. Lattice Theory: First Concepts and Distributive Lattices. San Francisco, CA: W. H. Freeman, 1971.
Grätzer, G. Universal Algebra, 2nd ed. New York: Springer-Verlag, 1979.
Grätzer, G. General Lattice Theory, 2nd ed. Boston, MA: Birkhäuser, 1998.
Hobby, D. and McKenzie, R. The Structure of Finite Algebras. Providence, RI: Amer. Math. Soc., 1988.
Insall, E. "Nonstandard Methods and Finiteness Conditions in Algebra." Ph.D. dissertation. Houston, TX: University of Houston, 1989.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.
Insall, M. "Geometric Conditions for Local Finiteness of a Lattice of Convex Sets." Math. Moravica 1, 35-40, 1997.
Schweigert, D. "Central Relations on Lattices." J. Austral. Math. Soc. 37, 213-219, 1988.
Schweigert, D. and Szymanska, M. "On Central Relations of Complete Lattices." Czech. Math. J. 37, 70-74, 1987.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|