


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-10-2021
Date: 29-11-2021
Date: 30-8-2021
|
A differential evolution method used to minimize functions of real variables. Evolution strategies are significantly faster at numerical optimization than traditional genetic algorithms and also more likely to find a function's true global extremum.
These methods heuristically "mimic" biological evolution: namely, the process of natural selection and the "survival of the fittest" principle. An adaptive search procedure based on a "population" of candidate solution points is used. Iterations involve a competitive selection that drops the poorer solutions. The remaining pool of candidates with higher "fitness value" are then "recombined" with other solutions by swapping components with another; they can also be "mutated" by making some smaller-scale change to a candidate. The recombination and mutation moves are applied sequentially; their aim is to generate new solutions that are biased towards subsets of 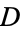 in which good, although not necessarily globally optimized, solutions have already been found. Numerous variants of this general strategy based on diverse evolution "game rules" can be constructed. The different types of evolutionary search methods include approaches that are aimed at continuous global optimization problems, and also others that are targeted towards solving combinatorial problems. The latter group is often called genetic algorithms (Goldberg 1989, Michalewicz 1996, Osman and Kelly 1996, Voss et al. 1999).
in which good, although not necessarily globally optimized, solutions have already been found. Numerous variants of this general strategy based on diverse evolution "game rules" can be constructed. The different types of evolutionary search methods include approaches that are aimed at continuous global optimization problems, and also others that are targeted towards solving combinatorial problems. The latter group is often called genetic algorithms (Goldberg 1989, Michalewicz 1996, Osman and Kelly 1996, Voss et al. 1999).
REFERENCES:
Corne, D.; Dorigo, M.; and Glover, F. New Ideas in Optimization. New York: McGraw-Hill, 1999.
Goldberg, D. E. Genetic Algorithms in Search, Optimization, and Machine Learning. Reading, MA: Addison-Wesley, 1989.
Jacob, C. Illustrating Evolutionary Computation with Mathematica. San Francisco, CA: Morgan Kaufmann, 2001.
Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs, 3rd ed. Berlin: Springer-Verlag, 1996.
Osman, I. H. and Kelly, J. P. (Eds.). Meta-Heuristics: Theory and Applications. Dordrecht, Netherlands: Kluwer, 1996.
Price, K. and Storn, R. "Differential Evolution." Dr. Dobb's J., Issue 264, 18-24 and 78, Apr. 1997.
Voss, S.; Martello, S.; Osman, I. H.; and Roucairol, C. (Eds.). Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization. Dordrecht, Netherlands: Kluwer, 1999.



|
|
|
|
لمكافحة الاكتئاب.. عليك بالمشي يوميا هذه المسافة
|
|
|
|
|
|
|
تحذيرات من ثوران بركاني هائل قد يفاجئ العالم قريبا
|
|
|
|
|
|
|
العتبة العباسية تشارك في معرض النجف الأشرف الدولي للتسوق الشامل
|
|
|