
Quasi-Minimal Residual Method
 المؤلف:
Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H.
المؤلف:
Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H.
 المصدر:
Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.
المصدر:
Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 1-12-2021
1-12-2021
 1667
1667
Quasi-Minimal Residual Method
The biconjugate gradient method often displays rather irregular convergence behavior. Moreover, the implicit LU decomposition of the reduced tridiagonal system may not exist, resulting in a breakdown of the algorithm. The quasi-minimal residual method (Freund and Nachtigal 1991) is a related algorithm that attempts to overcome these problems.
The main idea behind the quasi-minimal residual (QMR) method algorithm is to solve the reduced tridiagonal system in a least squares sense, similar to the approach followed in the generalized minimal residual method (GMRES). Since the constructed basis for the Krylov subspace is biorthogonal, rather than orthogonal as in GMRES, the obtained solution is viewed as a quasi-minimal residual solution, which explains the name. Additionally, QMR uses look-ahead techniques to avoid breakdowns in the underlying Lanczos process, which makes it more robust than the biconjugate gradient method.
The convergence behavior of QMR is typically much smoother than for the biconjugate gradient method (BCG). Freund and Nachtigal (1991) present quite general error bounds which show that QMR may be expected to converge about as fast as the generalized minimal residual method. From a relation between the residuals in BCG and QMR (Freund and Nachtigal 1991, relation 5.10) one may deduce that at phases in the iteration process where BCG makes significant progress, QMR has arrived at about the same approximation for  . On the other hand, when BCG makes no progress at all, QMR may still show slow convergence.
. On the other hand, when BCG makes no progress at all, QMR may still show slow convergence.
The look-ahead steps in this version of the QMR method prevent breakdown in all cases except the so-called "incurable breakdown," where no practical number of look-ahead steps would yield a next iterate.
The pseudocode for the preconditioned quasi-minimal residual method with preconditioner 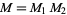 is given above. This algorithm follows the two term recurrence version without look-ahead (Freund and Nachtigal 1994, Algorithm 7.1). This version of QMR is simpler to implement than the full QMR method with look-ahead, but it is susceptible to breakdown of the underlying Lanczos process. (Other implementation variations are whether to scale Lanczos vectors or not, or to use three-term recurrences instead of coupled two-term recurrences. Such decisions usually have implications for the stability and the efficiency of the algorithm.)
is given above. This algorithm follows the two term recurrence version without look-ahead (Freund and Nachtigal 1994, Algorithm 7.1). This version of QMR is simpler to implement than the full QMR method with look-ahead, but it is susceptible to breakdown of the underlying Lanczos process. (Other implementation variations are whether to scale Lanczos vectors or not, or to use three-term recurrences instead of coupled two-term recurrences. Such decisions usually have implications for the stability and the efficiency of the algorithm.)
Computation of the residual is done for the convergence test. If one uses right (or post) preconditioning, that is 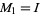 , then a cheap upper bound for
, then a cheap upper bound for 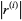 can be computed in each iteration, avoiding the recursions for
can be computed in each iteration, avoiding the recursions for 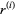 (Freund and Nachtigal 1991, Proposition 4.1). This upper bound may be pessimistic by a factor of at most
(Freund and Nachtigal 1991, Proposition 4.1). This upper bound may be pessimistic by a factor of at most 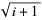 .
.
QMR has roughly the same problems with respect to vector and parallel implementation as the biconjugate gradient method. The scalar overhead per iteration is slightly more than for BCG. In all cases where the slightly cheaper BCG method converges irregularly (but fast enough), QMR may be preferred for stability reasons.
REFERENCES:
Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.
Freund, R. and Nachtigal, N. "QMR: A Quasi-Minimal Residual Method for Non-Hermitian Linear Systems." Numer. Math. 60, 315-339, 1991.
Freund, R. and Nachtigal, N. "An Implementation of the QMR Method Based on Coupled Two-Term Recurrences." SIAM J. Sci. Statist. Comput. 15, 313-337, 1994.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


