

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Finite Difference
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Differences." §25.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
28-11-2021
2578
Finite Difference
The finite difference is the discrete analog of the derivative. The finite forward difference of a function 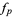 is defined as
is defined as
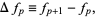 |
(1) |
and the finite backward difference as
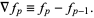 |
(2) |
The forward finite difference is implemented in the Wolfram Language as DifferenceDelta[f, i].
If the values are tabulated at spacings 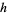 , then the notation
, then the notation
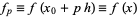 |
(3) |
is used. The 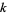 th forward difference would then be written as
th forward difference would then be written as 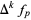 , and similarly, the
, and similarly, the 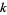 th backward difference as
th backward difference as 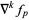 .
.
However, when 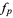 is viewed as a discretization of the continuous function
is viewed as a discretization of the continuous function 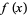 , then the finite difference is sometimes written
, then the finite difference is sometimes written
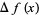 |
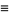 |
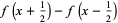 |
(4) |
 |
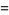 |
(5) |
where 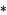 denotes convolution and
denotes convolution and {{0.101266, -0.101266}, {0.375, -0.375}}, BoxBaselineShift -> -0.375]AdjustmentBox[I, BoxMargins -> {{0, 0}, {-0.25, 0.25}}, BoxBaselineShift -> 0.25](x)" src="https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline16.gif" style="height:15px; width:33px" /> is the odd impulse pair. The finite difference operator can therefore be written
|
(6) |
An 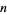 th power has a constant
th power has a constant 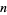 th finite difference. For example, take
th finite difference. For example, take 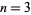 and make a difference table,
and make a difference table,
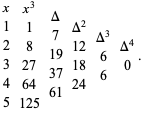 |
(7) |
The 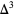 column is the constant 6.
column is the constant 6.
Finite difference formulas can be very useful for extrapolating a finite amount of data in an attempt to find the general term. Specifically, if a function 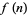 is known at only a few discrete values
is known at only a few discrete values 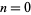 , 1, 2, ... and it is desired to determine the analytical form of
, 1, 2, ... and it is desired to determine the analytical form of 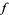 , the following procedure can be used if
, the following procedure can be used if 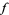 is assumed to be a polynomial function. Denote the
is assumed to be a polynomial function. Denote the 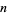 th value in the sequence of interest by
th value in the sequence of interest by 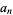 . Then define
. Then define 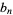 as the forward difference
as the forward difference 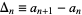 ,
, 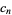 as the second forward difference
as the second forward difference 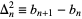 , etc., constructing a table as follows
, etc., constructing a table as follows
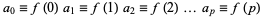 |
(8) |
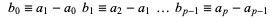 |
(9) |
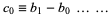 |
(10) |
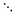 |
(11) |
Continue computing 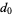 ,
, 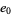 , etc., until a 0 value is obtained. Then the polynomial function giving the values
, etc., until a 0 value is obtained. Then the polynomial function giving the values 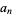 is given by
is given by
 |
 |
 |
(12) |
 |
 |
 |
(13) |
When the notation 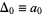 ,
, 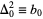 , etc., is used, this beautiful equation is called Newton's forward difference formula. To see a particular example, consider a sequence with first few values of 1, 19, 143, 607, 1789, 4211, and 8539. The difference table is then given by
, etc., is used, this beautiful equation is called Newton's forward difference formula. To see a particular example, consider a sequence with first few values of 1, 19, 143, 607, 1789, 4211, and 8539. The difference table is then given by
 |
(14) |
Reading off the first number in each row gives 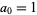 ,
, 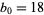 ,
, 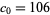 ,
, 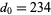 ,
, 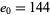 . Plugging these in gives the equation
. Plugging these in gives the equation
 |
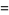 |
 |
(15) |
 |
 |
 |
(16) |
which indeed fits the original data exactly.
Formulas for the derivatives are given by
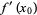 |
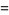 |
![1/h[f(x_0+h)-f(x_0)]-1/2hf^()(xi)](https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline59.gif) |
(17) |
 |
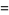 |
![1/(2h)[-3f(x_0)+4f(x_0+h)-f(x_0+2h)]+1/3h^2f^((3))(xi)](https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline62.gif) |
(18) |
 |
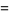 |
![1/(2h)[f(x_0+h)-f(x_0-h)]-1/6h^2f^((3))(xi)](https://mathworld.wolfram.com/images/equations/FiniteDifference/Inline65.gif) |
(19) |
 |
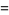 |
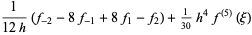 |
(20) |
 |
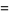 |
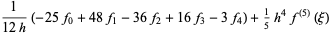 |
(21) |
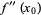 |
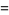 |
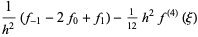 |
(22) |
 |
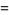 |
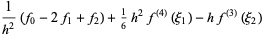 |
(23) |
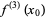 |
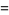 |
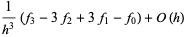 |
(24) |
 |
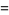 |
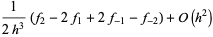 |
(25) |
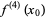 |
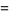 |
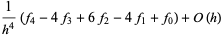 |
(26) |
 |
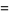 |
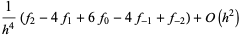 |
(27) |
(Beyer 1987, pp. 449-451; Zwillinger 1995, p. 705).
Formulas for integrals of finite differences
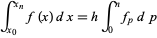 |
(28) |
are given by Beyer (1987, pp. 455-456).
Finite differences lead to difference equations, finite analogs of differential equations. In fact, umbral calculus displays many elegant analogs of well-known identities for continuous functions. Common finite difference schemes for partial differential equations include the so-called Crank-Nicolson, Du Fort-Frankel, and Laasonen methods.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Differences." §25.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 877-878, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 429-515, 1987.
Boole, G. and Moulton, J. F. A Treatise on the Calculus of Finite Differences, 2nd rev. ed. New York: Dover, 1960.
Conway, J. H. and Guy, R. K. "Newton's Useful Little Formula." In The Book of Numbers. New York: Springer-Verlag, pp. 81-83, 1996.
Fornberg, B. "Calculation of Weights in Finite Difference Formulas." SIAM Rev. 40, 685-691, 1998.
Iyanaga, S. and Kawada, Y. (Eds.). "Interpolation." Appendix A, Table 21 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1482-1483, 1980.
Jordan, C. Calculus of Finite Differences, 3rd ed. New York: Chelsea, 1965.
Levy, H. and Lessman, F. Finite Difference Equations. New York: Dover, 1992.
Milne-Thomson, L. M. The Calculus of Finite Differences. London: Macmillan, 1951.
Richardson, C. H. An Introduction to the Calculus of Finite Differences. New York: Van Nostrand, 1954.
Spiegel, M. Calculus of Finite Differences and Differential Equations. New York: McGraw-Hill, 1971.
Stirling, J. Methodus differentialis, sive tractatus de summation et interpolation serierum infinitarium. London, 1730. English translation by Holliday, J. The Differential Method: A Treatise of the Summation and Interpolation of Infinite Series. 1749.
Tweddle, C. James Stirling: A Sketch of His Life and Works Along with his Scientific Correspondence. Oxford, England: Oxford University Press, pp. 30-45, 1922.
Weisstein, E. W. "Books about Finite Difference Equations." http://www.ericweisstein.com/encyclopedias/books/FiniteDifferenceEquations.html.
Zwillinger, D. (Ed.). "Difference Equations" and "Numerical Differentiation." §3.9 and 8.3.2 in CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, pp. 228-235 and 705-705, 1995.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















