

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Devil,s Staircase
المؤلف:
Adams, W. W.
المصدر:
"A Remarkable Class of Continued Fractions." Proc. Amer. Math. Soc. 65
الجزء والصفحة:
...
16-9-2021
1304
Devil's Staircase
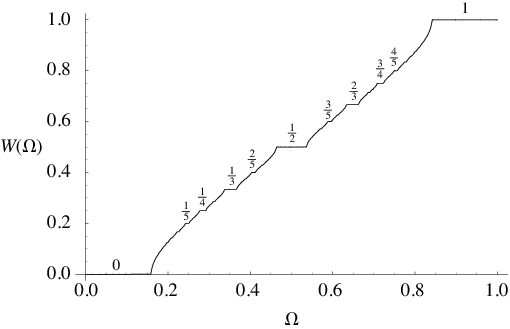
A plot of the map winding number 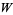 resulting from mode locking as a function of
resulting from mode locking as a function of 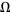 for the circle map
for the circle map
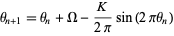 |
(1) |
with 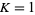 . (Since the circle map becomes mode-locked, the map winding number is independent of the initial starting argument
. (Since the circle map becomes mode-locked, the map winding number is independent of the initial starting argument 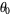 .) At each value of
.) At each value of 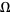 , the map winding number is some rational number. The result is a monotonic increasing "staircase" for which the simplest rational numbers have the largest steps. The Devil's staircase continuously maps the interval
, the map winding number is some rational number. The result is a monotonic increasing "staircase" for which the simplest rational numbers have the largest steps. The Devil's staircase continuously maps the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline6.gif) onto
onto ![[0,1]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline7.gif) , but is constant almost everywhere (i.e., except on a Cantor set).
, but is constant almost everywhere (i.e., except on a Cantor set).
For 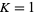 , the measure of quasiperiodic states (
, the measure of quasiperiodic states (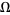 irrational) on the
irrational) on the 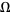 -axis has become zero, and the measure of mode-locked state has become 1. The dimension of the Devil's staircase
-axis has become zero, and the measure of mode-locked state has become 1. The dimension of the Devil's staircase 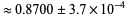 .
.
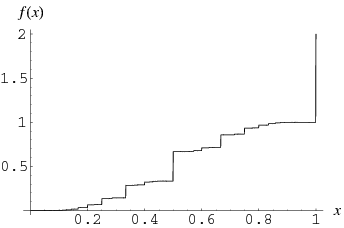
Another type of devil's staircase occurs for the sum
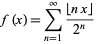 |
(2) |
for ![x in [0,1]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline12.gif) , where
, where 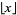 is the floor function (Böhmer 1926ab; Kuipers and Niederreiter 1974, p. 10; Danilov 1974; Adams 1977; Davison 1977; Bowman 1988; Borwein and Borwein 1993; Bowman 1995; Bailey and Crandall 2001; Bailey and Crandall 2003). This function is monotone increasing and continuous at every irrational
is the floor function (Böhmer 1926ab; Kuipers and Niederreiter 1974, p. 10; Danilov 1974; Adams 1977; Davison 1977; Bowman 1988; Borwein and Borwein 1993; Bowman 1995; Bailey and Crandall 2001; Bailey and Crandall 2003). This function is monotone increasing and continuous at every irrational  but discontinuous at every rational
but discontinuous at every rational  .
. 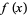 is irrational iff
is irrational iff  is, and if
is, and if  is irrational, then
is irrational, then 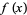 is transcendental. If
is transcendental. If 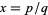 is rational, then
is rational, then
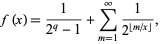 |
(3) |
while if  is irrational,
is irrational,
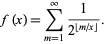 |
(4) |
Even more amazingly, for irrational  with simple continued fraction
with simple continued fraction ![[0,a_1,a_2,...]](https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline23.gif) and convergents
and convergents 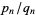 ,
,
![f(x)=[0,A_1,A_2,A_3,...],](https://mathworld.wolfram.com/images/equations/DevilsStaircase/NumberedEquation5.gif) |
(5) |
where
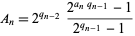 |
(6) |
(Bailey and Crandall 2001). This gives the beautiful relation to the Rabbit constant
![f(phi^(-1))=[0,2^(F_0),2^(F_1),2^(F_2),...],](https://mathworld.wolfram.com/images/equations/DevilsStaircase/NumberedEquation7.gif) |
(7) |
where 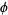 is the golden ratio and
is the golden ratio and 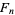 is a Fibonacci number.
is a Fibonacci number.
REFERENCES:
Adams, W. W. "A Remarkable Class of Continued Fractions." Proc. Amer. Math. Soc. 65, 194-198, 1977.
Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Böhmer, P. E. "Über die Transcendenz gewisser dyadischer Brüche." Math. Ann. 96, 367-377, 1926a.
Böhmer, P. E. Erratum to "Über die Transcendenz gewisser dyadischer Brüche." Math. Ann. 96, 735, 1926b.
Borwein, J. and Borwein, P. "On the Generating Function of the Integer Part of 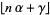 ." J. Number Th. 43, 293-318, 1993.
." J. Number Th. 43, 293-318, 1993.
Bowman, D. "A New Generalization of Davison's Theorem." Fib. Quart. 26, 40-45, 1988.
Bowman, D. "Approximation of 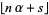 and the Zero of
and the Zero of {nalpha+s}" src="https://mathworld.wolfram.com/images/equations/DevilsStaircase/Inline29.gif" style="height:15px; width:49px" />." J. Number Th. 50, 128-144, 1995.
Danilov, L. V. "Some Classes of Transcendental Numbers." Math. Notes Acad. Sci. USSR 12, 524-527, 1974.
Davison, J. L. "A Series and Its Associated Continued Fraction." Proc. Amer. Math. Soc. 63, 29-32, 1977.
Devaney, R. L. An Introduction to Chaotic Dynamical Systems. Redwood City, CA: Addison-Wesley, pp. 109-110, 1987.
Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences. New York: Wiley, 1974.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 82-83 and 286-287, 1983.
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, 1993.
Rasband, S. N. "The Circle Map and the Devil's Staircase." §6.5 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 128-132, 1990.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















