A universal cellular automaton is a cellular automaton which, like a Turing machine, exhibits universality. von Neumann proved that an automaton consisting of cells with four orthogonal neighbors and 29 possible states would be capable of simulating a Turing machine for some configuration of about 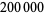 cells (Gardner 1983, p. 227).

The outlines of a proof that the two-dimensional game of life outer-totalistic cellular automaton is universal were given by Berlekamp, Conway, and Guy (1982) and independently by Gosper (Gardner 1983, pp. 250-253). Around 2000, a Turing machine was explicitly implemented in life by P. Rendell (Rendell, Adamatzky 2001). While Rendell's machine can be made into a "true" universal computer simply by making his tape infinite, he neither noted this fact nor provided an actual construction of a universal Turing machine. Subsequently, on November 11, 2002, P. Chapman constructed a game of life pattern that implements the actions of a universal register machine, thus explicitly proving the game of life to be universal.

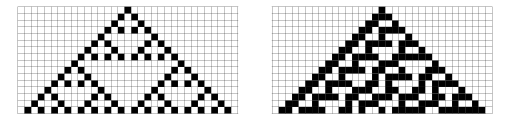
More amazingly still, even one-dimensional cellular automata can be universal. Wolfram (2002, pp. 644-656) gave an example of a 19-color universal one-dimensional next-nearest neighbor cellular automaton in which a block of 20 cells is used to represent each single cell in the cellular automaton being emulated. The examples above show the first few steps of the 19-color universal automaton emulating rule 90 and rule 30, respectively (Wolfram 2002, pp. 646-647).

Smith (1971) showed that 18 colors and nearest-neighbor 1-dimensional rules could be universal, and Lindgren and Nordahl (1990) constructed a 7-color nearest-neighbor universal cellular automaton. And most amazingly of all, as shown by Wolfram (2002, pp. 675-691), two colors and nearest neighbor rules are sufficient for producing universality in a 1-dimensional cellular automaton. In particular, although it is anything but straightforward to prove, the rule 110 elementary cellular automaton is universal (Cook 2004).

Gacs (2001) has proven that there exist fault-tolerant universal cellular automata, whose ability to simulate other cellular automata is not hindered by random perturbations provided that such perturbations are sufficiently sparse.

REFERENCES:

Adamatzky, A. (Ed.). Collision Based Computing. Mult.-Valued Log. 6, pp. 397-514, 2001. Yverdon: Gordon and Breach, 2001.

Berlekamp, E. R.; Conway, J. H.; and Guy, R. K. "What Is Life?" Ch. 25 in Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular. London: Academic Press, 1982.

Chapman, P. "Life Universal Computer." http://www.igblan.com/ca/.

Cook, M. "Universality in Elementary Cellular Automata." Complex Systems 15, 1-40, 2004.

Gacs, P. "Reliable Cellular Automata with Self-Organization." J. Stat. Phys. 103, 45-267, 2001.

Gardner, M. "The Game of Life, Parts I-III." Chs. 20-22 in Wheels, Life, and other Mathematical Amusements. New York: W. H. Freeman, 1983.

Gray, L. "A Mathematician Looks at Wolfram's New Kind of Science." Not. Amer. Math. Soc. 50, 200-211, 2003.

Lindgren, K. and Nordahl, M. G. "Universal Computation in Simple One-Dimensional Cellular Automata." Complex Systems 4, 299-318, 1990.

Rendell, P. "This Is a Turing Machine Implemented in Conway's Game of Life." http://www.rendell.uk.co/gol/tm.htm.

Smith, A. R. III. "Simple Computation-Universal Cellular Spaces." J. Assoc. Comput. Mach. 18, 339-353, 1971.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 646-647, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد