Embedding

An embedding is a representation of a topological object, manifold, graph, field, etc. in a certain space in such a way that its connectivity or algebraic properties are preserved. For example, a field embedding preserves the algebraic structure of plus and times, an embedding of a topological space preserves open sets, and a graph embedding preserves connectivity.

One space 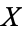 is embedded in another space  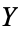when the properties of  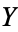restricted to  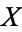are the same as the properties of 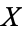. For example, the rationals are embedded in the reals, and the integers are embedded in the rationals. In geometry, the sphere is embedded in  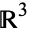as the unit sphere.

Let 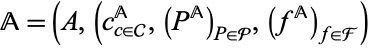 and 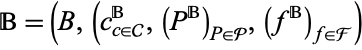 be structures for the same first-order language 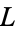, and let  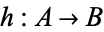be a homomorphism from  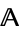to 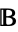. Then  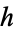is an embedding provided that it is injective (Enderton 1972, Grätzer 1979, Burris and Sankappanavar 1981).

For example, if 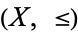 and 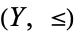 are partially ordered sets, then an injective monotone mapping  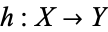may not be an embedding from  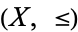into 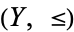. To be an embedding, such a mapping must preserve order "both ways":

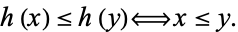REFERENCES:

Burris, S. and Sankappanavar, H. P. A Course in Universal Algebra. New York: Springer-Verlag, 1981. https://www.thoralf.uwaterloo.ca/htdocs/ualg.html.

Enderton, H. B. A Mathematical Introduction to Logic. New York: Academic Press, 1972.

Grätzer, G. Universal Algebra, 2nd ed. New York: Springer-Verlag, 1979.