Point-Set Topology 

The low-level language of topology, which is not really considered a separate "branch" of topology. Point-set topology, also called set-theoretic topology or general topology, is the study of the general abstract nature of continuity or "closeness" on spaces. Basic point-set topological notions are ones like continuity, dimension, compactness, and connectedness. The intermediate value theorem (which states that if a path in the real line connects two numbers, then it passes over every point between the two) is a basic topological result. Others are that Euclidean n-space is homeomorphic to Euclidean 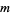-space iff 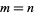, and that real valued functions achieve maxima and minima on compact sets.

Foundational point-set topological questions are ones like "when can a topology on a space be derived from a metric?" Point-set topology deals with differing notions of continuity and compares them, as well as dealing with their properties. Point-set topology is also the ground-level of inquiry into the geometrical properties of spaces and continuous functions between them, and in that sense, it is the foundation on which the remainder of topology (algebraic, differential, and low-dimensional) stands.

REFERENCES:

Bing, R. H. "Elementary Point Set Topology." Amer. Math. Monthly 67, 1960.

Ferreirós, J. "Origins of the Theory of Point-Sets." Ch. 5 in Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Basel, Switzerland: Birkhäuser, pp. 95-97, 1999.

Sutherland, W. A. An Introduction to Metric & Topological Spaces. New York: Oxford University Press, 1975.

Vaidyanathaswamy, R. Set Topology. New York: Dover, 1999.