


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-7-2021
Date: 16-6-2021
Date: 15-5-2021
|
The first example discovered of a map from a higher-dimensional sphere to a lower-dimensional sphere which is not null-homotopic. Its discovery was a shock to the mathematical community, since it was believed at the time that all such maps were null-homotopic, by analogy with homology groups.
The Hopf map 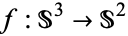 arises in many contexts, and can be generalized to a map
arises in many contexts, and can be generalized to a map 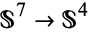 . For any point
. For any point 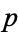 in the sphere, its preimage
in the sphere, its preimage 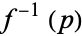 is a circle
is a circle 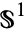 in
in 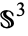 . There are several descriptions of the Hopf map, also called the Hopf fibration.
. There are several descriptions of the Hopf map, also called the Hopf fibration.
As a submanifold of 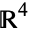 , the 3-sphere is
, the 3-sphere is
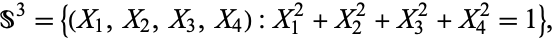 |
(1) |
and the 2-sphere is a submanifold of 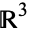 ,
,
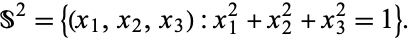 |
(2) |
The Hopf map takes points ( ,
,  ,
, 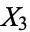 ,
, 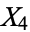 ) on a 3-sphere to points on a 2-sphere (
) on a 3-sphere to points on a 2-sphere (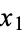 ,
, 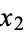 ,
, 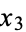 )
)
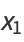 |
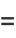 |
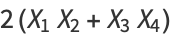 |
(3) |
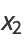 |
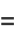 |
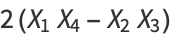 |
(4) |
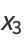 |
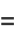 |
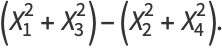 |
(5) |
Every point on the 2-sphere corresponds to a circle called the Hopf circle on the 3-sphere.
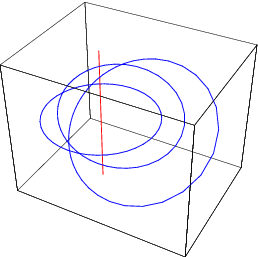
By stereographic projection, the 3-sphere can be mapped to 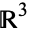 , where the point at infinity corresponds to the north pole. As a map, from
, where the point at infinity corresponds to the north pole. As a map, from 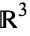 , the Hopf map can be pretty complicated. The diagram above shows some of the preimages
, the Hopf map can be pretty complicated. The diagram above shows some of the preimages 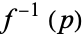 , called Hopf circles. The straight red line is the circle through infinity.
, called Hopf circles. The straight red line is the circle through infinity.
By associating 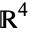 with
with 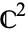 , the map is given by
, the map is given by 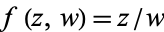 , which gives the map to the Riemann sphere.
, which gives the map to the Riemann sphere.
The Hopf fibration is a fibration
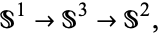 |
(6) |
and is in fact a principal bundle. The associated vector bundle
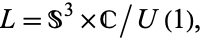 |
(7) |
where
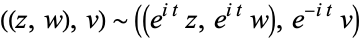 |
(8) |
is a complex line bundle on 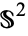 . In fact, the set of line bundles on the sphere forms a group under vector bundle tensor product, and the bundle
. In fact, the set of line bundles on the sphere forms a group under vector bundle tensor product, and the bundle 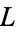 generates all of them. That is, every line bundle on the sphere is
generates all of them. That is, every line bundle on the sphere is 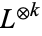 for some
for some 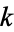 .
.
The sphere 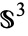 is the Lie group of unit quaternions, and can be identified with the special unitary group
is the Lie group of unit quaternions, and can be identified with the special unitary group 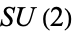 , which is the simply connected double cover of
, which is the simply connected double cover of 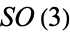 . The Hopf bundle is the quotient map
. The Hopf bundle is the quotient map 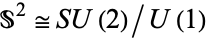 .
.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|