


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-9-2016
Date: 27-6-2021
Date: 6-5-2021
|
The Lebesgue covering dimension is an important dimension and one of the first dimensions investigated. It is defined in terms of covering sets, and is therefore also called the covering dimension (as well as the topological dimension).
A space has Lebesgue covering dimension 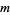 if for every open cover of that space, there is an open cover that refines it such that the refinement has order at most
if for every open cover of that space, there is an open cover that refines it such that the refinement has order at most 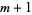 . Consider how many elements of the cover contain a given point in a base space. If this has a maximum over all the points in the base space, then this maximum is called the order of the cover. If a space does not have Lebesgue covering dimension
. Consider how many elements of the cover contain a given point in a base space. If this has a maximum over all the points in the base space, then this maximum is called the order of the cover. If a space does not have Lebesgue covering dimension 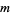 for any
for any 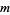 , it is said to be infinite dimensional.
, it is said to be infinite dimensional.
Results of this definition are:
1. Two homeomorphic spaces have the same dimension,
2. 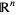 has dimension
has dimension 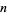 ,
,
3. A topological space can be embedded as a closed subspace of a Euclidean space iff it is locally compact, T2, second countable, and is finite-dimensional (in the sense of the Lebesgue covering dimension), and
4. Every compact metrizable 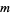 -dimensional topological space can be embedded in
-dimensional topological space can be embedded in 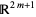 .
.
REFERENCES:
Dieudonne, J. A. A History of Algebraic and Differential Topology. Boston, MA: Birkhäuser, 1994.
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 414, 1980.
Munkres, J. R. Topology: A First Course, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|