


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-6-2017
Date: 15-6-2021
Date: 25-7-2021
|
A compact manifold is a manifold that is compact as a topological space. Examples are the circle (the only one-dimensional compact manifold) and the 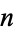 -dimensional sphere and torus. Compact manifolds in two dimensions are completely classified by their orientation and the number of holes (genus). It should be noted that the term "compact manifold" often implies "manifold without boundary," which is the sense in which it is used here. When there is need for a separate term, a compact boundaryless manifold is called a closed manifold.
-dimensional sphere and torus. Compact manifolds in two dimensions are completely classified by their orientation and the number of holes (genus). It should be noted that the term "compact manifold" often implies "manifold without boundary," which is the sense in which it is used here. When there is need for a separate term, a compact boundaryless manifold is called a closed manifold.
For many problems in topology and geometry, it is convenient to study compact manifolds because of their "nice" behavior. Among the properties making compact manifolds "nice" are the fact that they can be covered by finitely many coordinate charts, and that any continuous real-valued function is bounded on a compact manifold.
For any positive integer 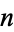 , a distinct nonorientable surface can be produced by replacing
, a distinct nonorientable surface can be produced by replacing 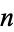 disks with Möbius strips. In particular, replacing one disk with a Möbius strip produces a cross surface and replacing two disks produces the Klein bottle. The sphere, the
disks with Möbius strips. In particular, replacing one disk with a Möbius strip produces a cross surface and replacing two disks produces the Klein bottle. The sphere, the 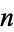 -holed tori, and this sequence of nonorientable surfaces form a complete list of compact, boundaryless two-dimensional manifolds.
-holed tori, and this sequence of nonorientable surfaces form a complete list of compact, boundaryless two-dimensional manifolds.

The following table lists the classes of two-dimensional compact manifolds for small 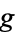 , which are also illustrated above.
, which are also illustrated above.
 |
0 | 1 | 2 |
| orientable | sphere | torus | double torus |
| nonorientable | cross surface | Klein bottle |
REFERENCES:
Armstrong, M. A. Basic Topology, rev. ed. New York: Springer-Verlag, 1997.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|