


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-6-2021
Date: 25-6-2017
Date: 7-7-2021
|
Let 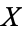 and
and 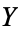 be CW-complexes, and let
be CW-complexes, and let 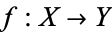 be a continuous map. Then the cellular approximation theorem states that any such
be a continuous map. Then the cellular approximation theorem states that any such 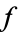 is homotopic to a cellular map. In fact, if the map
is homotopic to a cellular map. In fact, if the map 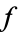 is already cellular on a CW-subcomplex
is already cellular on a CW-subcomplex 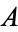 of
of 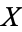 , then the homotopy can be taken to be stationary on
, then the homotopy can be taken to be stationary on 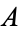 .
.
A famous application of the theorem is the calculation of some homotopy groups of 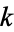 -spheres
-spheres 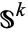 . Indeed, let
. Indeed, let 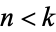 and bestow on both
and bestow on both 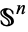 and
and 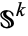 their usual CW-structure, with one
their usual CW-structure, with one 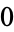 -cell, and one
-cell, and one 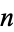 -cell, respectively one
-cell, respectively one 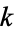 -cell. If
-cell. If 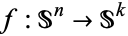 is a continuous, base-point preserving map, then by cellular approximation, it is homotopic to a cellular map
is a continuous, base-point preserving map, then by cellular approximation, it is homotopic to a cellular map 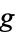 . This map
. This map  must map the
must map the  -skeleton of
-skeleton of 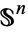 into the
into the 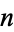 -skeleton of
-skeleton of 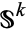 , but the
, but the 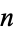 -skeleton of
-skeleton of 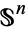 is
is 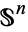 itself, while the
itself, while the 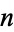 -skeleton of
-skeleton of 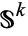 is the zero-cell, i.e., a point. This is because of the condition
is the zero-cell, i.e., a point. This is because of the condition 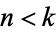 . Thus
. Thus 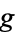 is a constant map, whence
is a constant map, whence 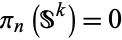 .
.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|