


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2021
Date: 15-6-2021
Date: 10-6-2021
|
Given a compact manifold 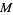 and a transversely orientable codimension-one foliation
and a transversely orientable codimension-one foliation 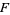 on
on 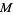 which is tangent to
which is tangent to 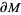 , the pair
, the pair 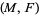 is called a generalized Reeb component if the holonomy groups of all leaves in the interior
is called a generalized Reeb component if the holonomy groups of all leaves in the interior 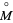 are trivial and if all leaves of
are trivial and if all leaves of 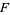 are proper. Generalized Reeb components are obvious generalizations of Reeb components.
are proper. Generalized Reeb components are obvious generalizations of Reeb components.
The introduction of the generalized version of the Reeb component facilitates the proof of many significant results in the theory of 3-manifolds and of foliations. It is well-known that generalized Reeb components are transversely orientable and that a manifold 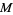 admitting a generalized Reeb component also admits a nice vector field
admitting a generalized Reeb component also admits a nice vector field 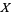 (Imanishi and Yagi 1976). Moreover, given a generalized Reeb component
(Imanishi and Yagi 1976). Moreover, given a generalized Reeb component 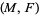 ,
, 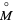 is a fibration over
is a fibration over 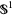 .
.
Like many notions in geometric topology, the generalized Reeb component can be presented in various contexts. One source describes a generalized Reeb component on a closed 3-manifold 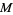 with foliation
with foliation 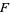 to be a submanifold
to be a submanifold 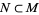 of maximal dimension which is bounded by tori
of maximal dimension which is bounded by tori 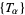 such that the orientation of these tori as leaves of
such that the orientation of these tori as leaves of 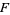 is the same as (or simultaneously opposite to) their orientation as the boundary components of
is the same as (or simultaneously opposite to) their orientation as the boundary components of 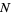 (Eliashberg and Thurston 1998). Framed in this way, generalized Reeb components are shown to have deep connections to various notions in foliation theory, e.g., in presenting an existence criterion for a closed 3-manifold
(Eliashberg and Thurston 1998). Framed in this way, generalized Reeb components are shown to have deep connections to various notions in foliation theory, e.g., in presenting an existence criterion for a closed 3-manifold 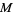 to admit a taut foliation.
to admit a taut foliation.
REFERENCES:
Eliashberg, Y. M. and Thurston, W. P. Confoliations. Providence, RI: Amer. Math. Soc., 1998.
Goodman, S. "Closed Leaves in Foliations of Codimension One." Comm. Math. Helv. 50, 383-388, 1975.
Imanishi, H. and Yagi, K. "On Reeb Components." J. Math. Kyoto Univ. 16, 313-324, 1976.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|