


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-3-2021
Date: 17-3-2021
Date: 12-4-2021
|

The binomial distribution gives the discrete probability distribution 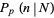 of obtaining exactly
of obtaining exactly 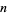 successes out of
successes out of 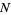 Bernoulli trials (where the result of each Bernoulli trial is true with probability
Bernoulli trials (where the result of each Bernoulli trial is true with probability 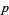 and false with probability
and false with probability 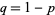 ). The binomial distribution is therefore given by
). The binomial distribution is therefore given by
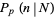 |
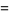 |
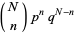 |
(1) |
 |
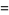 |
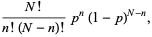 |
(2) |
where 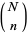 is a binomial coefficient. The above plot shows the distribution of
is a binomial coefficient. The above plot shows the distribution of 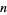 successes out of
successes out of 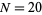 trials with
trials with 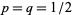 .
.
The binomial distribution is implemented in the Wolfram Language as BinomialDistribution[n, p].
The probability of obtaining more successes than the 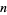 observed in a binomial distribution is
observed in a binomial distribution is
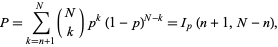 |
(3) |
where
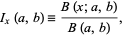 |
(4) |
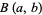 is the beta function, and
is the beta function, and 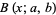 is the incomplete beta function.
is the incomplete beta function.
The characteristic function for the binomial distribution is
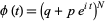 |
(5) |
(Papoulis 1984, p. 154). The moment-generating function 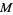 for the distribution is
for the distribution is
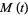 |
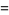 |
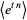 |
(6) |
 |
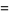 |
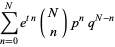 |
(7) |
 |
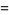 |
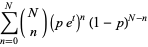 |
(8) |
 |
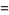 |
![[pe^t+(1-p)]^N](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline31.gif) |
(9) |
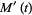 |
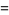 |
![N[pe^t+(1-p)]^(N-1)(pe^t)](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline34.gif) |
(10) |
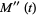 |
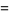 |
![N(N-1)[pe^t+(1-p)]^(N-2)(pe^t)^2+N[pe^t+(1-p)]^(N-1)(pe^t).](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline37.gif) |
(11) |
The mean is
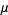 |
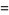 |
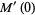 |
(12) |
 |
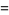 |
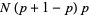 |
(13) |
 |
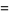 |
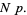 |
(14) |
The moments about 0 are
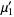 |
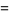 |
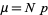 |
(15) |
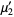 |
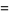 |
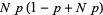 |
(16) |
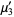 |
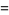 |
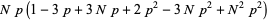 |
(17) |
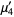 |
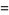 |
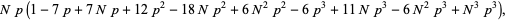 |
(18) |
so the moments about the mean are
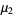 |
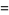 |
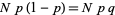 |
(19) |
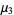 |
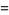 |
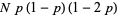 |
(20) |
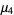 |
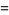 |
![Np(1-p)[3p^2(2-N)+3p(N-2)+1].](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline67.gif) |
(21) |
The skewness and kurtosis excess are
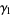 |
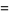 |
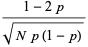 |
(22) |
 |
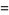 |
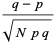 |
(23) |
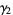 |
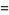 |
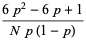 |
(24) |
 |
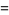 |
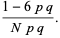 |
(25) |
The first cumulant is
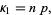 |
(26) |
and subsequent cumulants are given by the recurrence relation
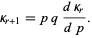 |
(27) |
The mean deviation is given by
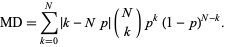 |
(28) |
For the special case 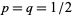 , this is equal to
, this is equal to
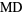 |
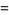 |
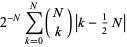 |
(29) |
 |
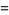 |
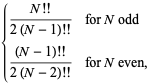 |
(30) |
where 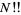 is a double factorial. For
is a double factorial. For 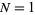 , 2, ..., the first few values are therefore 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, ... (OEIS A086116 and A086117). The general case is given by
, 2, ..., the first few values are therefore 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, ... (OEIS A086116 and A086117). The general case is given by
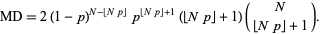 |
(31) |
Steinhaus (1999, pp. 25-28) considers the expected number of squares 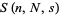 containing a given number of grains
containing a given number of grains 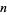 on board of size
on board of size 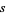 after random distribution of
after random distribution of 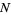 of grains,
of grains,
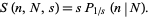 |
(32) |
Taking 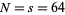 gives the results summarized in the following table.
gives the results summarized in the following table.
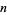 |
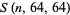 |
| 0 | 23.3591 |
| 1 | 23.7299 |
| 2 | 11.8650 |
| 3 | 3.89221 |
| 4 | 0.942162 |
| 5 | 0.179459 |
| 6 | 0.0280109 |
| 7 | 0.0036840 |
| 8 | 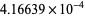 |
| 9 | 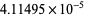 |
| 10 | 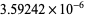 |
An approximation to the binomial distribution for large 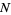 can be obtained by expanding about the value
can be obtained by expanding about the value 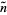 where
where 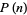 is a maximum, i.e., where
is a maximum, i.e., where 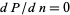 . Since the logarithm function is monotonic, we can instead choose to expand the logarithm. Let
. Since the logarithm function is monotonic, we can instead choose to expand the logarithm. Let 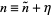 , then
, then
![ln[P(n)]=ln[P(n^~)]+B_1eta+1/2B_2eta^2+1/(3!)B_3eta^3+...,](https://mathworld.wolfram.com/images/equations/BinomialDistribution/NumberedEquation9.gif) |
(33) |
where
![B_k=[(d^kln[P(n)])/(dn^k)]_(n=n^~).](https://mathworld.wolfram.com/images/equations/BinomialDistribution/NumberedEquation10.gif) |
(34) |
But we are expanding about the maximum, so, by definition,
![B_1=[(dln[P(n)])/(dn)]_(n=n^~)=0.](https://mathworld.wolfram.com/images/equations/BinomialDistribution/NumberedEquation11.gif) |
(35) |
This also means that 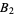 is negative, so we can write
is negative, so we can write 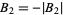 . Now, taking the logarithm of (◇) gives
. Now, taking the logarithm of (◇) gives
![ln[P(n)]=lnN!-lnn!-ln(N-n)!+nlnp+(N-n)lnq.](https://mathworld.wolfram.com/images/equations/BinomialDistribution/NumberedEquation12.gif) |
(36) |
For large 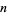 and
and 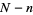 we can use Stirling's approximation
we can use Stirling's approximation
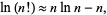 |
(37) |
so
![(d[ln(n!)])/(dn)](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline108.gif) |
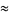 |
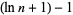 |
(38) |
 |
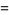 |
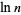 |
(39) |
![(d[ln(N-n)!])/(dn)](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline114.gif) |
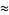 |
![d/(dn)[(N-n)ln(N-n)-(N-n)]](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline116.gif) |
(40) |
 |
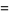 |
![[-ln(N-n)+(N-n)(-1)/(N-n)+1]](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline119.gif) |
(41) |
 |
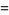 |
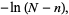 |
(42) |
and
![(dln[P(n)])/(dn) approx -lnn+ln(N-n)+lnp-lnq.](https://mathworld.wolfram.com/images/equations/BinomialDistribution/NumberedEquation14.gif) |
(43) |
To find 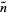 , set this expression to 0 and solve for
, set this expression to 0 and solve for 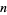 ,
,
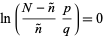 |
(44) |
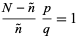 |
(45) |
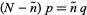 |
(46) |
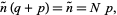 |
(47) |
since 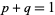 . We can now find the terms in the expansion
. We can now find the terms in the expansion
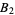 |
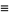 |
![[(d^2ln[P(n)])/(dn^2)]_(n=n^~)](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline128.gif) |
(48) |
 |
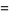 |
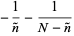 |
(49) |
 |
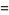 |
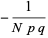 |
(50) |
 |
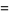 |
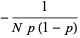 |
(51) |
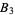 |
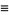 |
![[(d^3ln[P(n)])/(dn^3)]_(n=n^~)](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline140.gif) |
(52) |
 |
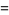 |
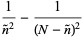 |
(53) |
 |
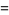 |
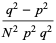 |
(54) |
 |
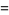 |
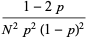 |
(55) |
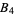 |
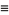 |
![[(d^4ln[P(n)])/(dn^4)]_(n=n^~)](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline152.gif) |
(56) |
 |
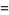 |
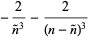 |
(57) |
 |
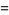 |
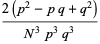 |
(58) |
 |
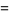 |
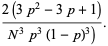 |
(59) |
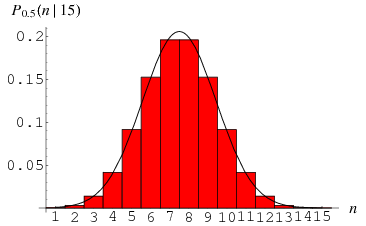
Now, treating the distribution as continuous,
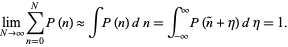 |
(60) |
Since each term is of order 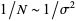 smaller than the previous, we can ignore terms higher than
smaller than the previous, we can ignore terms higher than 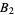 , so
, so
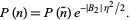 |
(61) |
The probability must be normalized, so
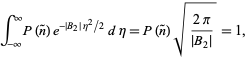 |
(62) |
and
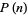 |
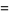 |
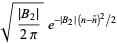 |
(63) |
 |
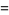 |
![1/(sqrt(2piNpq))exp[-((n-Np)^2)/(2Npq)].](https://mathworld.wolfram.com/images/equations/BinomialDistribution/Inline169.gif) |
(64) |
Defining 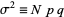 ,
,
![P(n)=1/(sigmasqrt(2pi))exp[-((n-n^~)^2)/(2sigma^2)],](https://mathworld.wolfram.com/images/equations/BinomialDistribution/NumberedEquation22.gif) |
(65) |
which is a normal distribution. The binomial distribution is therefore approximated by a normal distribution for any fixed 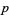 (even if
(even if 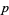 is small) as
is small) as 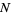 is taken to infinity.
is taken to infinity.
If 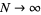 and
and 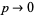 in such a way that
in such a way that 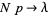 , then the binomial distribution converges to the Poisson distribution with mean
, then the binomial distribution converges to the Poisson distribution with mean 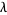 .
.
Let  and
and 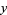 be independent binomial random variables characterized by parameters
be independent binomial random variables characterized by parameters 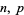 and
and 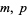 . The conditional probability of
. The conditional probability of  given that
given that 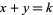 is
is
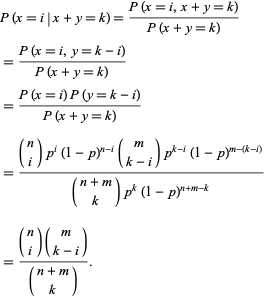 |
(66) |
Note that this is a hypergeometric distribution.
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 531, 1987.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 102-103, 1984.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution." §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 219-223, 1992.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 108-109, 1992.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|