


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-4-2021
Date: 28-3-2021
Date: 14-2-2021
|
A uniform distribution, sometimes also known as a rectangular distribution, is a distribution that has constant probability.

The probability density function and cumulative distribution function for a continuous uniform distribution on the interval ![[a,b]](https://mathworld.wolfram.com/images/equations/UniformDistribution/Inline1.gif) are
are
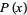 |
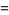 |
 |
(1) |
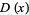 |
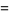 |
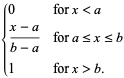 |
(2) |
These can be written in terms of the Heaviside step function 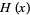 as
as
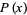 |
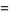 |
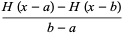 |
(3) |
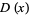 |
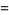 |
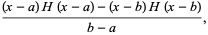 |
(4) |
the latter of which simplifies to the expected 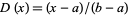 for
for 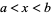 .
.
The continuous distribution is implemented as UniformDistribution[a, b].
For a continuous uniform distribution, the characteristic function is
![phi(t)=2/((b-a)t)sin[1/2(b-a)t]e^(i(a+b)t/2).](https://mathworld.wolfram.com/images/equations/UniformDistribution/NumberedEquation1.gif) |
(5) |
If 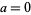 and
and 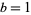 , the characteristic function simplifies to
, the characteristic function simplifies to
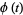 |
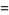 |
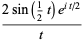 |
(6) |
 |
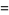 |
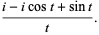 |
(7) |
The moment-generating function is
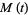 |
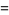 |
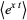 |
(8) |
 |
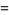 |
![int_a^b(e^(xt))/(b-a)dx=[(e^(xt))/(t(b-a))]_a^b](https://mathworld.wolfram.com/images/equations/UniformDistribution/Inline30.gif) |
(9) |
 |
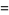 |
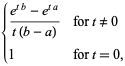 |
(10) |
and
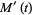 |
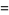 |
![1/(b-a)[1/t(be^(bt)-ae^(at))-1/(t^2)(e^(bt)-e^(at))]](https://mathworld.wolfram.com/images/equations/UniformDistribution/Inline36.gif) |
(11) |
 |
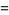 |
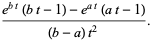 |
(12) |
The moment-generating function is not differentiable at zero, but the moments can be calculated by differentiating and then taking 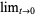 . The raw moments are given analytically by
. The raw moments are given analytically by
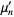 |
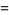 |
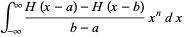 |
(13) |
 |
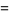 |
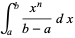 |
(14) |
 |
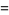 |
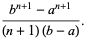 |
(15) |
The first few are therefore given explicitly by
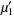 |
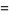 |
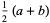 |
(16) |
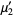 |
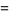 |
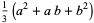 |
(17) |
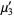 |
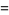 |
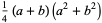 |
(18) |
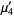 |
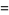 |
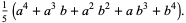 |
(19) |
The central moments are given analytically by
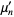 |
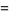 |
![int_(-infty)^infty(H(x-a)-H(x-b))/(b-a)[x-1/2(a+b)]^ndx](https://mathworld.wolfram.com/images/equations/UniformDistribution/Inline64.gif) |
(20) |
 |
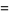 |
![int_a^b([x-1/2(a+b)]^n)/(b-a)dx](https://mathworld.wolfram.com/images/equations/UniformDistribution/Inline67.gif) |
(21) |
 |
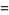 |
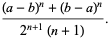 |
(22) |
The first few are therefore given explicitly by
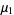 |
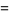 |
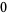 |
(23) |
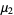 |
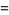 |
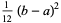 |
(24) |
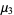 |
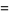 |
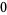 |
(25) |
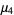 |
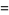 |
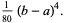 |
(26) |
The mean, variance, skewness, and kurtosis excess are therefore
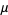 |
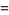 |
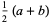 |
(27) |
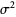 |
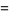 |
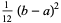 |
(28) |
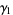 |
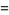 |
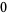 |
(29) |
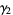 |
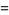 |
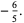 |
(30) |
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 531 and 533, 1987.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|