


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-1-2016
Date: 5-5-2021
Date: 8-2-2021
|
The 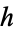 -statistic
-statistic 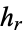 is the unique symmetric unbiased estimator for a central moment of a distribution
is the unique symmetric unbiased estimator for a central moment of a distribution
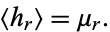 |
(1) |
In addition, the variance
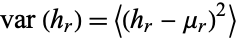 |
(2) |
is a minimum compared to all other unbiased estimators (Halmos 1946; Rose and Smith 2002, p. 254). The first few are given in terms of power sums by
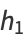 |
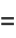 |
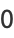 |
(3) |
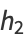 |
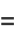 |
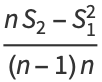 |
(4) |
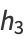 |
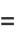 |
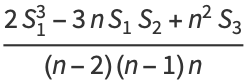 |
(5) |
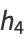 |
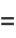 |
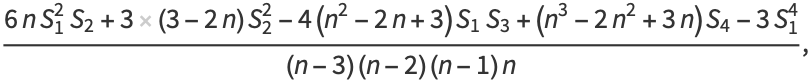 |
(6) |
and in terms of sample central moments by
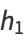 |
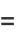 |
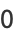 |
(7) |
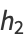 |
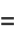 |
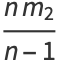 |
(8) |
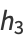 |
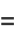 |
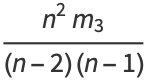 |
(9) |
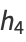 |
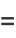 |
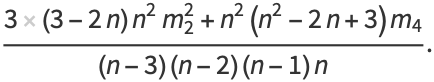 |
(10) |
These can be given by HStatistic[r] and HStatisticToSampleCentral[r], respectively, in the Wolfram Language application package mathStatica.
REFERENCES:
Dwyer, P. S. "Moments of Any Rational Integral Isobaric Sample Moment Function." Ann. Math. Stat. 8, 21-65, 1937.
Halmos, P. R. "The Theory of Unbiased Estimation." Ann. Math. Stat. 17, 34-43, 1946.
Rose, C. and Smith, M. D. "h-Statistics: Unbiased Estimators of Central Moments." §7.2B in Mathematical Statistics with Mathematica. New York: Springer-Verlag, pp. 253-256, 2002.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|