


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2021
Date: 20-2-2021
Date: 10-2-2021
|
A real-valued stochastic process 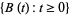 is a Brownian motion which starts at
is a Brownian motion which starts at 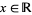 if the following properties are satisfied:
if the following properties are satisfied:
1. 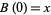 .
.
2. For all times 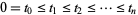 , the increments
, the increments 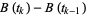 ,
, 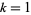 , ...,
, ..., 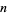 , are independent random variables.
, are independent random variables.
3. For all 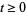 ,
, 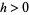 , the increments
, the increments 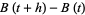 are normally distributed with expectation value zero and variance
are normally distributed with expectation value zero and variance 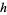 .
.
4. The function 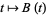 is continuous almost everywhere. The Brownian motion
is continuous almost everywhere. The Brownian motion 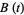 is said to be standard if
is said to be standard if 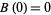 .
.
It is easily shown from the above criteria that a Brownian motion has a number of unique natural invariance properties including scaling invariance and invariance under time inversion. Moreover, any Brownian motion 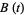 satisfies a law of large numbers so that
satisfies a law of large numbers so that
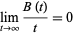 |
almost everywhere. Moreover, despite looking ill-behaved at first glance, Brownian motions are Hölder continuous almost everywhere for all values 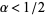 . Contrarily, any Brownian motion is nowhere differentiable almost surely.
. Contrarily, any Brownian motion is nowhere differentiable almost surely.
The above definition is extended naturally to get higher-dimensional Brownian motions. More precisely, given independent Brownian motions 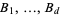 which start at
which start at 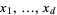 , one can define a stochastic process
, one can define a stochastic process 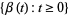 by
by
![beta(t)=[B_1(t); |; B_d(t)].](https://mathworld.wolfram.com/images/equations/BrownianMotion/NumberedEquation2.gif) |
Such a 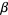 is called a
is called a 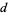 -dimensional Brownian motion which starts at
-dimensional Brownian motion which starts at 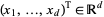 .
.
REFERENCES:
Mörters, P. and Peres, Y. "Brownian Motion." 2008. http://www.stat.berkeley.edu/~peres/bmbook.pdf.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|