


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-4-2021
Date: 17-3-2021
Date: 3-5-2021
|
The randomization of a deck of cards by repeated interleaving. More generally, a shuffle is a rearrangement of the elements in an ordered list. Shuffling by exactly interleaving two halves of a deck is called a riffle shuffle. Shuffling by successively interchanging the cards in position 1, 2, ..., 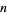 with cards in randomly chosen positions is known as an exchange shuffle. Normal shuffling leaves gaps of different lengths between the two layers of cards and so randomizes the order of the cards.
with cards in randomly chosen positions is known as an exchange shuffle. Normal shuffling leaves gaps of different lengths between the two layers of cards and so randomizes the order of the cards.
Keller (1995) showed that roughly 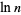 shuffles are needed just to randomize the bottom card.
shuffles are needed just to randomize the bottom card.
REFERENCES:
Aldous, D. and Diaconis, P. "Shuffling Cards and Stopping Times." Amer. Math. Monthly 93, 333-348, 1986.
Bayer, D. and Diaconis, P. "Trailing the Dovetail Shuffle to Its Lair." Ann. Appl. Probability 2, 294-313, 1992.
Brualdi, R. and Ryser, H. J. Combinatorial Matrix Theory. New York: Cambridge University Press, 1991.
Goldstein, D. and Moews, D. "The Identity Is the Most Likely Exchange Shuffle for Large 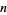 ." 6 Oct 2000. https://arxiv.org/abs/math.CO/0010066.
." 6 Oct 2000. https://arxiv.org/abs/math.CO/0010066.
Keller, J. B. "How Many Shuffles to Mix a Deck?" SIAM Review 37, 88-89, 1995.
Morris, S. B. "Practitioner's Commentary: Card Shuffling." UMAP J. 15, 333-338, 1994.
Morris, S. B. Magic Tricks, Card Shuffling, and Dynamic Computer Memories. Washington, DC: Math. Assoc. Amer., 1998.
Rosenthal, J. W. "Card Shuffling." Math. Mag. 54, 64-67, 1981.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|