


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-2-2021
Date: 22-3-2021
Date: 28-2-2021
|
Let 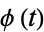 be the characteristic function, defined as the Fourier transform of the probability density function
be the characteristic function, defined as the Fourier transform of the probability density function 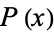 using Fourier transform parameters
using Fourier transform parameters 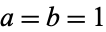 ,
,
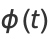 |
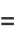 |
](https://mathworld.wolfram.com/images/equations/Cumulant/Inline6.gif) |
(1) |
 |
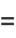 |
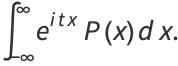 |
(2) |
The cumulants 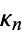 are then defined by
are then defined by
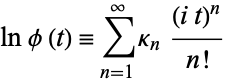 |
(3) |
(Abramowitz and Stegun 1972, p. 928). Taking the Maclaurin series gives
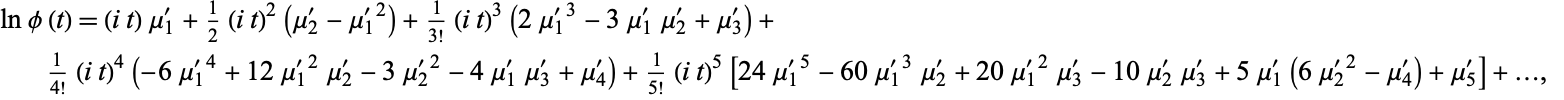 |
(4) |
where 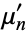 are raw moments, so
are raw moments, so
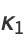 |
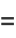 |
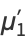 |
(5) |
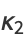 |
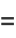 |
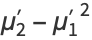 |
(6) |
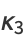 |
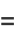 |
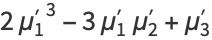 |
(7) |
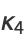 |
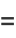 |
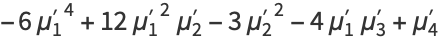 |
(8) |
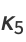 |
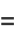 |
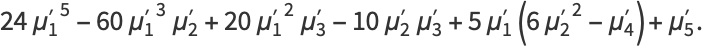 |
(9) |
These transformations can be given by CumulantToRaw[n] in the Mathematica application package mathStatica.
In terms of the central moments 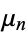 ,
,
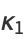 |
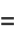 |
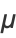 |
(10) |
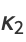 |
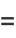 |
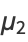 |
(11) |
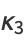 |
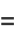 |
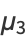 |
(12) |
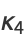 |
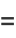 |
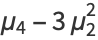 |
(13) |
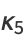 |
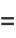 |
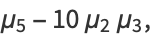 |
(14) |
where 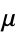 is the mean and
is the mean and 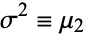 is the variance. These transformations can be given by CumulantToCentral[n].
is the variance. These transformations can be given by CumulantToCentral[n].
Multivariate cumulants can be expressed in terms of raw moments, e.g.,
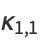 |
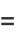 |
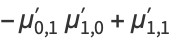 |
(15) |
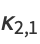 |
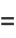 |
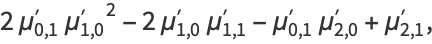 |
(16) |
and central moments, e.g.,
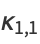 |
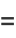 |
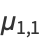 |
(17) |
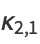 |
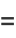 |
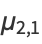 |
(18) |
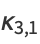 |
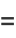 |
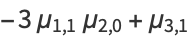 |
(19) |
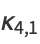 |
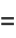 |
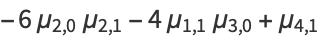 |
(20) |
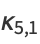 |
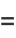 |
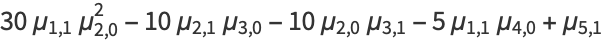 |
(21) |
using CumulantToRaw[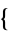 m, n, ...
m, n, ...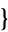 ] and CumulantToCentral[
] and CumulantToCentral[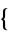 m, n, ...
m, n, ...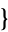 ], respectively.
], respectively.
The k-statistics are unbiased estimators of the cumulants.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 928, 1972.
Kenney, J. F. and Keeping, E. S. "Cumulants and the Cumulant-Generating Function," "Additive Property of Cumulants," and "Sheppard's Correction." §4.10-4.12 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 77-82, 1951.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|