

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Random Number
المؤلف:
Bassein, S.
المصدر:
"A Sampler of Randomness." Amer. Math. Monthly 103
الجزء والصفحة:
...
22-3-2021
4622
Random Number
A random number is a number chosen as if by chance from some specified distribution such that selection of a large set of these numbers reproduces the underlying distribution. Almost always, such numbers are also required to be independent, so that there are no correlations between successive numbers. Computer-generated random numbers are sometimes called pseudorandom numbers, while the term "random" is reserved for the output of unpredictable physical processes. When used without qualification, the word "random" usually means "random with a uniform distribution." Other distributions are of course possible. For example, the Box-Muller transformation allows pairs of uniform random numbers to be transformed to corresponding random numbers having a two-dimensional normal distribution.
It is impossible to produce an arbitrarily long string of random digits and prove it is random. Strangely, it is also very difficult for humans to produce a string of random digits, and computer programs can be written which, on average, actually predict some of the digits humans will write down based on previous ones.
There are a number of common methods used for generating pseudorandom numbers, the simplest of which is the linear congruence method. Another simple and elegant method is elementary cellular automaton rule 30, whose central column is given by 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1, ... (OEIS A051023), and which provides the random number generator used for large integers in the Wolfram Language. Most random number generators require specification of an initial number used as the starting point, which is known as a "seed." The goodness of random numbers generated by a given algorithm can be analyzed by examining its noise sphere.
When generating random numbers over some specified boundary, it is often necessary to normalize the distributions so that each differential area is equally populated. For example, picking 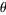 and
and 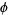 from uniform distributions does not give a uniform distribution for sphere point picking.
from uniform distributions does not give a uniform distribution for sphere point picking.
In order to generate a power-law distribution 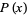 from a uniform distribution
from a uniform distribution 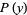 , write
, write 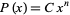 for
for ![x in [x_0,x_1]](https://mathworld.wolfram.com/images/equations/RandomNumber/Inline6.gif) . Then normalization gives
. Then normalization gives
![int_(x_0)^(x_1)P(x)dx=C([x^(n+1)]_(x_0)^(x_1))/(n+1)=1,](https://mathworld.wolfram.com/images/equations/RandomNumber/NumberedEquation1.gif) |
(1) |
so
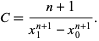 |
(2) |
Let 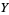 be a uniformly distributed variate on
be a uniformly distributed variate on ![[0,1]](https://mathworld.wolfram.com/images/equations/RandomNumber/Inline8.gif) . Then
. Then
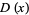 |
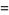 |
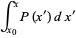 |
(3) |
 |
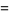 |
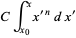 |
(4) |
 |
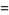 |
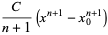 |
(5) |
 |
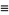 |
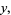 |
(6) |
and the variate given by
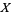 |
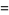 |
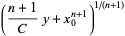 |
(7) |
 |
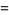 |
![[(x_1^(n+1)-x_0^(n+1))y+x_0^(n+1)]^(1/(n+1))](https://mathworld.wolfram.com/images/equations/RandomNumber/Inline26.gif) |
(8) |
is distributed as 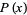 .
.
REFERENCES:
Bassein, S. "A Sampler of Randomness." Amer. Math. Monthly 103, 483-490, 1996.
Bennett, D. J. Randomness. Cambridge, MA: Harvard University Press, 1998.
Bratley, P.; Fox, B. L.; and Schrage, E. L. A Guide to Simulation, 2nd ed. New York: Springer-Verlag, 1996.
Dahlquist, G. and Bjorck, A. Ch. 11 in Numerical Methods. Englewood Cliffs, NJ: Prentice-Hall, 1974.
Deak, I. Random Number Generators and Simulation. New York: State Mutual Book & Periodical Service, 1990.
Evans, M.; Hastings, N.; and Peacock, B. Statistical Distributions, 3rd ed. New York: Wiley, p. 5, 2000.
Forsythe, G. E.; Malcolm, M. A.; and Moler, C. B. Ch. 10 in Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977.
Gardner, M. "Random Numbers." Ch. 13 in Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage, pp. 161-172, 1977.
James, F. "A Review of Pseudorandom Number Generators." Computer Physics Comm. 60, 329-344, 1990.
Kac, M. "What is Random?" Amer. Sci. 71, 405-406, 1983.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 200-201 and 205-207, 1962.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 151-154, 1951.
Knuth, D. E. Ch. 3 in The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Marsaglia, G. "A Current View of Random Number Generators." In Computer Science and Statistics: Proceedings of the Symposium on the Interface, 16th, Atlanta, Georgia, March 1984 (Ed. L. Billard). New York: Elsevier, 1985.
Marsaglia, G. "DIEHARD: A Battery of Tests for Random Number Generators." https://stat.fsu.edu/~geo/diehard.html.
Mascagni, M. "Random Numbers on the Web." https://archive.ncsa.uiuc.edu/Apps/CMP/RNG/mascagni/www-rng.html.
Niederreiter, H. Random Number Generation and Quasi-Monte Carlo Methods. Philadelphia, PA: SIAM, 1992.
Nijenhuis, A. and Wilf, H. Combinatorial Algorithms for Computers and Calculators, 2nd ed. New York: Academic Press, 1978.
Park, S. and Miller, K. "Random Number Generators: Good Ones are Hard to Find." Comm. ACM 31, 1192-1201, 1988.
Peterson, I. The Jungles of Randomness: A Mathematical Safari. New York: Wiley, 1997.
Pickover, C. A. "Computers, Randomness, Mind, and Infinity." Ch. 31 in Keys to Infinity. New York: W. H. Freeman, pp. 233-247, 1995.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Random Numbers." Ch. 7 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 266-306, 1992.
Schrage, L. "A More Portable Fortran Random Number Generator." ACM Trans. Math. Software 5, 132-138, 1979.
Schroeder, M. "Random Number Generators." In Number Theory in Science and Communication, with Applications in Cryptography, Physics, Digital Information, Computing and Self-Similarity, 3rd ed. New York: Springer-Verlag, pp. 289-295, 1990.
Sloane, N. J. A. Sequence A051023 in "The On-Line Encyclopedia of Integer Sequences."
Weisstein, E. W. "Books about Randomness." https://www.ericweisstein.com/encyclopedias/books/Randomness.html.
Wilf, H. S. Combinatorial Algorithms: An Update. Philadelphia, PA: SIAM, 1989.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















