Round Number

A round number is a number that is the product of a considerable number of comparatively small factors (Hardy 1999, p. 48). Round numbers are very rare. As Hardy (1999, p. 48) notes, "Half the numbers are divisible by 2, one-third by 3, one-sixth by both 2 and 3, and so on. Surely, then we may expect most numbers to have a large number of factors. But the facts seem to show the opposite."

A positive integer 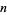 is sometimes said to be round (or "square root-smooth") if it has no prime factors greater than 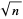. The first few such numbers are 1, 4, 8, 9, 12, 16, 18, 24, 25, 27, 30, 32, ... (OEIS A048098). Using this definition, an asymptotic formula for the number of round integers less than or equal to a positive real number  is given by

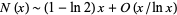(Hildebrand).

A different meaning of "round" is used when speaking of "rounding a number."

REFERENCES:

Hardy, G. H. "Round Numbers." Ch. 3 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 48-57, 1999.

Hildebrand, A. J. "Analytic Number Theory Problem Set 4. Solutions." https://www.math.uiuc.edu/~hildebr/531/hw4sol.pdf.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 89-90, 1998.

Sloane, N. J. A. Sequences A048098 in "The On-Line Encyclopedia of Integer Sequences."