المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Bernoulli Triangle |
 1225
 03:38 مساءً
date: 6-1-2021 |
Author : MacWilliams, F. J. and Sloane, N. J. A. 
Book or Source : The Theory of Error-Correcting Codes. Amsterdam, Netherlands: North-Holland 
Page and Part : ...|
Read More
Date: 10-4-2020
1054
Date: 25-8-2020
1112
Date: 22-10-2019
883
|
 |
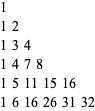(1) |
The number triangle illustrated above (OEIS A008949) composed of the partial sums of binomial coefficients,
 |
 |
 |
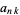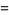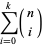(2) |
 |
 |
 |
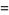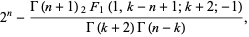(3) |
where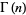 
is a gamma function and 
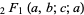is a hypergeometric function.
The plot above shows the binary representations for the first 255 (top figure) and 511 (bottom figure) terms of a flattened Bernoulli triangle.
REFERENCES:
Kirillov, A. A. "Variations on the Triangular Theme." In Lie Groups and Lie Algebras: E. B. Dynkin's Seminar: Dedicated to E. B. Dynkin on the Occasion of His Seventieth Birthday (Ed. S. G. Gindikin and E. B. Vinberg.) Providence, RI: Amer. Math. Soc., pp. 43-73, 1995.
MacWilliams, F. J. and Sloane, N. J. A. The Theory of Error-Correcting Codes. Amsterdam, Netherlands: North-Holland, p. 376, 1978.
Sloane, N. J. A. Sequence A008949 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|
