Littlewood Conjecture

The Littlewood conjecture states that for any two real numbers ,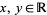

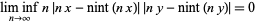where 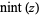 denotes the nearest integer function.

In layman's terms, this conjecture concerns the simultaneous approximation of two real numbers by rationals, indeed saying that any two real numbers  and 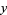 can be simultaneously approximated at least moderately well by rationals having the same denominator (Venkatesh 2007).

Though proof of the Littlewood conjecture still remains an open problem, many partial results exist. For example, Borel showed that the set of exceptional pairs 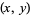 of real numbers  and 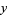 for which the conjecture fails has Lebesgue measure zero. Much later, Einsiedler et al. (2006) proved that the set of pairs of exceptional points also has Hausdorff dimension zero.

REFERENCES:

Einsiedler, M.; Katok, A.; and Lindenstrauss, E. "Invariant Measures and the Set of Exceptions to Littlewood's Conjecture." Ann. Math. 164, 513-560, 2006.

Venkatesh, A. "The Work of Einsiedler, Katok, and Lindenstrauss on the Littlewood Conjecture." Bull. Amer. Math. Soc., 45, 117-134, 2008.