Consecutive Number Sequences

Consecutive number sequences are sequences constructed by concatenating numbers of a given type. Many of these sequences were considered by Smarandache and so are sometimes known as Smarandache sequences.

The most obvious consecutive number sequence is the sequence of the first 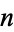 positive integers joined left-to-right, namely 1, 12, 123, 1234, ... (OEIS A007908; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 1; Mudge 1995; Stephan 1998; Wolfram 2002, p. 913). In this work, members of this sequence will be termed Smarandache numbers and the 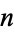th such number written 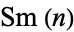. No Smarandache primes  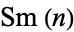exist for  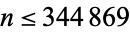(Great Smarandache PRPrime search; Dec. 5, 2016).

The 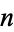th term  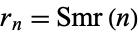of the "reverse integer sequence" consists of the concatenation of the first  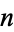positive integers written right-to-left: 1, 21, 321, 4321, ... (OEIS A000422; Smarandache 1993, Dumitrescu and Seleacu 1994, Stephan 1998). The terms up to  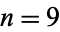are given by

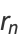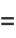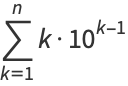			(1)
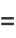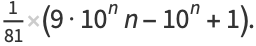			(2)

The terms of the reverse integer sequence have the same number of digits as the consecutive integer sequence. The first few reverse integer concatenated primes occur for 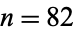 and 37765 (OEIS A176024), as summarized in the following table. No other primes occur for  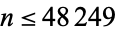(E. Weisstein, Nov. 10, 2015) or  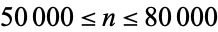(Batalov, Nov. 9, 2015).

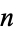	digits	discoverer
82	155	Stephan (1998), Fleuren (1999)
37765	177719	E. W. Weisstein (Apr. 6, 2010)

There is an amazing connection between the numbers 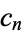, , 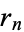the Demlo numbers, and the repunits.

The concatenation of the first 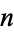 primes is called a Smarandache-Wellin number, the first few of which are 2, 23, 235, 2357, 235711, ... (OEIS A019518). The first few Smarandache-Wellin primes are 2, 23, 2357, ... (OEIS A069151), corresponding to concatenations of the first 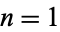, 2, 4, 128, 174, 342, 435, 1429 (OEIS A046035) primes and having 1, 2, 4, 355, 499, 1171, 1543, 5719 (OEIS A263959) decimal digits.

If digit sequences corresponding to concatenation of a right-truncated final prime are allowed, more primes are possible. In fact, these are precisely the Copeland-Erdős-constant primes, the first few of which are 2, 23, 2357, 23571113171, ... (OEIS A227529) and which have 1, 2, 4, 11, 353, 355, 499, 1171, 1543, 5719, 11048, 68433, 97855, 292447, ... decimal digits (OEIS A227530).

The concatenation of the first 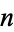 odd numbers gives 1, 13, 135, 1357, 13579, ... (OEIS A019519; Smith 1996, Marimutha 1997, Mudge 1997). This sequence is prime for terms 2, 10, 16, 34, 49, 2570, ... (OEIS A046036; Weisstein, Ibstedt 1998, pp. 75-76), with no others less than  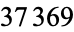(Weisstein, Oct. 9, 2015). The corresponding primes are 13, 135791113151719, 135791113151719212325272931, ... (OEIS A048847). The 2570th term, given by 1 3 5 7...5137 5139, has 9725 digits and was discovered by Weisstein in Aug. 1998.

The concatenation of the first 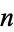 even numbers gives 2, 24, 246, 2468, 246810, ... (OEIS A019520; Smith 1996; Marimutha 1997; Mudge 1997; Ibstedt 1998, pp. 77-78).

The concatenation of the first 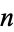 square numbers gives 1, 14, 149, 14916, ... (OEIS A019521; Marimutha 1997). The only prime in the first  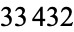terms is the third term, 149, (Weisstein, Oct. 9, 2015).

The concatenation of the first 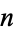 triangular numbers gives 1, 13, 136, 13610, ... (OEIS A078795). The only primes in the first  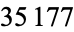terms occur for terms 2 and 6, corresponding to primes 13 and 136101521 (OEIS A158750; Weisstein, Oct. 9, 2015).

The concatenation of the first 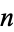 cubic numbers gives 1, 18, 1827, 182764, ... (OEIS A019522; Marimutha 1997). There are no primes in the first  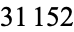terms (Weisstein, Oct. 9, 2009).

The concatenation of the first 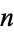 Fibonacci numbers gives 1, 11, 112, 1123, 11235, ... (OEIS A019523; Marimutha 1997). There are no primes in the first 1580 terms other than  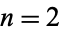and 4, corresponding to primes 11 and 1123 (E. Weisstein, Jul. 15, 2016).

REFERENCES:

--. "The Great Smarandache PRPrime search." https://smarandache.ddns.net:1200/server_stats.html.

Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, 2003.

Balatov, S. "RE: lovely open problem." Oct. 18, 2015. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind1510&L=NMBRTHRY&F=&S=&P=7439.

Balatov, S. Nov. 9, 2015. https://www.mersenneforum.org/showpost.php?p=415559&postcount=17.

Dumitrescu, C. and Seleacu, V. (Eds.). Some Notions and Questions in Number Theory. Glendale, AZ: Erhus University Press, 1994.

Fleuren, M. "Smarandache Factors and Reverse Factors." Smarandache Notions J. 10, 5-38, 1999.

Ibstedt, H. "Smarandache Concatenated Sequences." Ch. 5 in Computer Analysis of Number Sequences. Lupton, AZ: American Research Press, pp. 75-79, 1998.

Marimutha, H. "Smarandache Concatenate Type Sequences." Bull. Pure Appl. Sci. 16E, 225-226, 1997.

Mudge, M. "Top of the Class." Personal Computer World, 674-675, June 1995.

Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.

Rivera, C. "Problems & Puzzles: Puzzle 008-Primes by Listing." https://www.primepuzzles.net/puzzles/puzz_008.htm.

Sloane, N. J. A. Sequences A000422, A007908, A019518, A019519, A019520, A019521, A019522, A019523, A046035, A046036, A046284, A048847, A069151, A071620, A078795, A158750, A176024, A176942, A227529, and A227530 in "The On-Line Encyclopedia of Integer Sequences."

Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.

Smith, S. "A Set of Conjectures on Smarandache Sequences." Bull. Pure Appl. Sci. 15E, 101-107, 1996.

Stephan, R. W. "Factors and Primes in Two Smarandache Sequences." Smarandache Notions J. 9, 4-10, 1998.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 913, 2002.