


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2020
Date: 27-8-2020
Date: 19-2-2020
|
The sequence 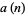 given by the exponents of the highest power of 2 dividing
given by the exponents of the highest power of 2 dividing 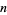 , i.e., the number of trailing 0s in the binary representation of
, i.e., the number of trailing 0s in the binary representation of 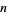 . For
. For 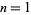 , 2, ..., the first few are 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, ... (OEIS A007814).
, 2, ..., the first few are 0, 1, 0, 2, 0, 1, 0, 3, 0, 1, 0, 2, ... (OEIS A007814).
Amazingly, this corresponds to one less than the number of disks to be moved at 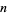 th step in the optimal solution to the tower of Hanoi problem: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, ... (OEIS A001511). The parity of this sequence is given by 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, ... (OEIS A035263) which, amazingly, also corresponds to the accumulation point of
th step in the optimal solution to the tower of Hanoi problem: 1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, ... (OEIS A001511). The parity of this sequence is given by 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, ... (OEIS A035263) which, amazingly, also corresponds to the accumulation point of 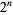 cycles through successive bifurcations.
cycles through successive bifurcations.
REFERENCES:
Atanassov, K. "On the 37th and the 38th Smarandache Problems. Notes on Number Theory and Discrete Mathematics, Sophia, Bulgaria 5, 83-85, 1999.
Atanassov, K. On Some of the Smarandache's Problems. Lupton, AZ: American Research Press, pp. 16-21, 1999.
Derrida, B.; Gervois, A.; and Pomeau, Y. "Iteration of Endomorphisms on the Real Axis and Representation of Number." Ann. Inst. Henri Poincaré, Section A: Physique Théorique 29, 305-356, 1978.
Karamanos, K. and Nicolis, G. "Symbolic Dynamics and Entropy Analysis of Feigenbaum Limit Sets." Chaos, Solitons, Fractals 10, 1135-1150, 1999.
Metropolis, M.; Stein, M. L.; and Stein, P. R. "On Finite Limit Sets for Transformations on the Unit Interval." J. Combin. Th. A 15, 25-44, 1973.
Sloane, N. J. A. Sequences A001511/M0127, A007814, and A035263 in "The On-Line Encyclopedia of Integer Sequences."
Smarandache, F. Only Problems, Not Solutions!, 4th ed. Phoenix, AZ: Xiquan, 1993.
Vitanyi, P. M. B. "An Optimal Simulation of Counter Machines." SIAM J. Comput. 14, 1-33, 1985.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|