Bernstein's Constant

Let 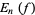 be the error of the best uniform approximation to a real function  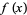on the interval  by real polynomials of degree at most 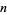. If

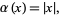(1)

then Bernstein showed that

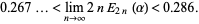(2)

He conjectured that the lower limit (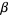) was 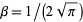. However, this was disproven by Varga and Carpenter (1987) and Varga (1990), who computed

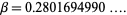(3)

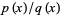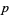For rational approximations  for  and 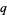 of degree  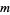and 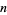, D. J. Newman (1964) proved

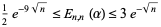(4)

for 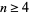. Gonchar (1967) and Bulanov (1975) improved the lower bound to

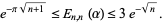(5)

Vjacheslavo (1975) proved the existence of positive constants 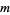 and 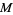 such that

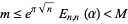(6)

(Petrushev 1987, pp. 105-106). Varga et al. (1993) conjectured and Stahl (1993) proved that

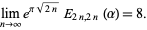(7)

REFERENCES:

Bernstein, S. N. "Sur la meilleure approximation de 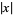 par les polynomes de degrés donnés." Acta Math. 37, 1-57, 1913.

Bulanov, A. P. "Asymptotics for the Best Rational Approximation of the Function Sign ." Mat. Sbornik 96, 171-178, 1975. English translation in Math. USSR Sbornik 5, 275-290, 1968.

Finch, S. R. "Bernstein's Constant." §4.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 257-259, 2003.

Gonchar, A. A. "Estimates for the Growth of Rational Functions and their Applications." Mat. Sbornik 72, 489-503, 1967.

Newman, D. J. "Rational Approximation to 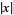." Michigan Math. J. 11, 11-14, 1964.

Petrushev, P. P. and Popov, V. A. Rational Approximation of Real Functions. New York: Cambridge University Press, 1987.

Stahl, H. "Best Uniform Rational Approximation of 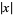 on ." Russian Acad. Sci. Sb. Math. 76, 461-487, 1993.

Stahl, H. Uniform Rational Approximation of 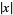. New York: Springer-Verlag, pp. 110-130, 1993.

Varga, R. S. Scientific Computations on Mathematical Problems and Conjectures. Philadelphia, PA: SIAM, 1990.

Varga, R. S. and Carpenter, A. J. "On a Conjecture of S. Bernstein in Approximation Theory." Math. USSR Sbornik 57, 547-560, 1987.

Varga, R. S.; Ruttan, A.; and Carpenter, A. J. "Numerical Results on Best Uniform Rational Approximations to 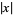 on . Mat. Sbornik 182, 1523-1541, 1991. English translation in Math. USSR Sbornik 74, 271-290, 1993.

Vjacheslavo, N. S. "On the Uniform Approximation of 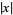 by Rational Functions." Dokl. Akad. Nauk SSSR 220, 512-515, 1975. English translation in Soviet Math. Dokl. 16, 100-104, 1975.