


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-1-2020
Date: 24-12-2019
Date: 2-9-2020
|
A semiprime which English economist and logician William Stanley Jevons incorrectly believed no one else would be able to factor. According to Jevons (1874, p. 123), "Can the reader say what two numbers multiplied together will produce the number 8616460799? I think it unlikely that anyone but myself will ever know."
Actually, a modern computer can factor this number in a few milliseconds as the product of two five-digit numbers:
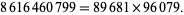 |
Published factorizations include those by Lehmer (1903) and Golomb (1996).
REFERENCES:
Golomb, S. W. "On the Factorization of Jevons' Number." Cryptologia 20, 243-244, Jul. 1996.
Jevons, W. S. The Principles of Science: A Treatise on Logic and Scientific Method. London: Macmillan, 1874. Reprinted by Kessinger, 2007.
Lehmer, D. N. "A Theorem in the Theory of Numbers." Read before the San Francisco Section of the American Mathematical Society. Dec. 19, 1903.
Žerovnik, J. "The RSA Cryptosystem in 1873." Obzornik Mat. Fiz. 43, 116-118, 1996.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|