Bauer's Identical Congruence

Let 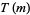 denote the set of the  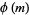numbers less than and relatively prime to 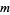, where  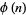is the totient function. Define

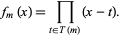(1)

Then a theorem of Lagrange states that

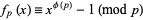(2)

for 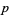 an odd prime (Hardy and Wright 1979, p. 98). Actually, this relationship holds for some composite values as well. Value for which it holds are 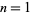, 3, 4, 5, 6, 7, 10, 11, 13, 17, 19, 23, 29, ... (OEIS A158008).

This can be generalized as follows. Let 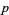 be an odd prime divisor of  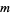and 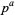 the highest power which divides 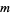, then

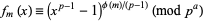(3)

and, in particular,

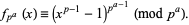(4)

Now, if 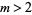 is even and  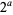is the highest power of 2 that divides 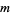, then

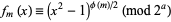(5)

and, in particular,

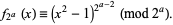(6)

REFERENCES:

Bauer. Nouvelles annales 2, 256-264, 1902.

Hardy, G. H. and Wright, E. M. J. London Math. Soc. 9, 38-41 and 240, 1934.

Hardy, G. H. and Wright, E. M. "Bauer's Identical Congruence." §8.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 98-100, 1979.

Sloane, N. J. A. Sequence A158008 in "The On-Line Encyclopedia of Integer Sequences."