Fundamental Region

Let 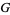 be a subgroup of the modular group Gamma. Then an open subset  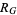of the upper half-plane  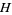is called a fundamental region o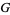f  if

1. No two distinct points of 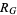 are equivalent under ,

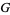2. If 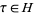, then there is a point  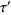in the closure of  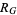such that  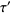is equivalent to  under .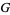

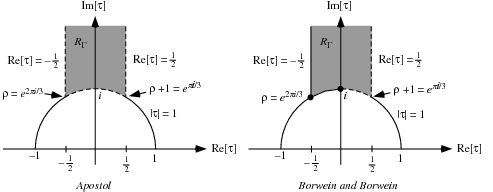
A fundamental region 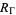 of the modular group Gamma is given by  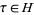such that  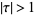and 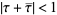, illustrated above, where  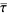is the complex conjugate of  (Apostol 1997, p. 31). Borwein and Borwein (1987, p. 113) define the boundaries of the region slightly differently by including the boundary points with .

REFERENCES:

Apostol, T. M. "Fundamental Region." §2.3 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 30-34, 1997.

Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 112-113, 1987.