


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-12-2020
Date: 5-6-2020
Date: 27-2-2020
|
An exponential sum of the form
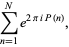 |
(1) |
where 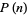 is a real polynomial (Weyl 1914, 1916; Montgomery 2001). Writing
is a real polynomial (Weyl 1914, 1916; Montgomery 2001). Writing
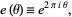 |
(2) |
a notation introduced by Vinogradov, Weyl observed that
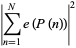 |
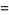 |
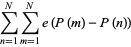 |
(3) |
 |
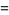 |
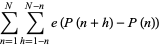 |
(4) |
 |
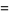 |
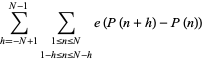 |
(5) |
 |
 |
![N+2R[sum_(h=1)^(N-1)sum_(n=1)^(N-h)e(P(n+h)-P(n))],](http://mathworld.wolfram.com/images/equations/WeylSum/Inline13.gif) |
(6) |
a process known as Weyl differencing (Montgomery 2001).
Weyl was able to use this process to show that if
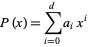 |
(7) |
is a real polynomial and at least one of 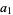 , ...,
, ..., 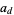 is irrational, then
is irrational, then 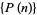 is uniformly distributed (mod 1).
is uniformly distributed (mod 1).
REFERENCES:
Berry, M. V. and Goldberg, J. "Renormalisation of Curlicues." Nonlinearity 61, 1-26, 1988.
Lehmer, D. H. and Lehmer, E. "Picturesque Exponential Sums, I." Amer. Math. Monthly 86, 725-733, 1979.
Montgomery, H. L. "Harmonic Analysis as Found in Analytic Number Theory." In Twentieth Century Harmonic Analysis--A Celebration. Proceedings of the NATO Advanced Study Institute Held in Il Ciocco, July 2-15, 2000 (Ed. J. S. Byrnes). Dordrecht, Netherlands: Kluwer, pp. 271-293, 2001.
Montgomery, H. L. Ten Lectures on the Interface between Analytic Number Theory and Harmonic Analysis. Providence, RI: Amer. Math. Soc., 1994.
Pickover, C. A. "Is the Fractal Golden Curlicue Cold?" Visual Comput. 11, 309-312, 1995.
Stewart, I. Another Fine Math You've Got Me Into.... New York: Freeman, 1992.
Weyl, H. "Über ein Problem aus dem Gebiete der diophantischen Approximationen." Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl., 234-244, 1914. Reprinted in Gesammelte Abhandlungen, Band I. Berlin: Springer-Verlag, pp. 487-497, 1968.
Weyl, H. "Über die Gleichverteilung von Zahlen mod. Eins." Math. Ann. 77, 313-352, 1916. Reprinted in Gesammelte Abhandlungen, Band I. Berlin: Springer-Verlag, pp. 563-599, 1968. Also reprinted in Selecta Hermann Weyl. Basel, Switzerland: Birkhäuser, pp. 111-147, 1956.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
أولياء أمور الطلبة يشيدون بمبادرة العتبة العباسية بتكريم الأوائل في المراحل المنتهية
|
|
|