المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Power Equation |
 790
 04:24 مساءً
date: 5-6-2020 |
Author : Dunn, A 
Book or Source : Mathematical Bafflers. New York: Dover 
Page and Part : ...|
Read More
Date: 10-9-2020
1366
Date: 12-10-2020
596
Date: 14-11-2019
606
|
Consider solutions to the equation
 |
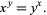(1) |
Real solutions are given by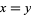 
for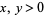 
, together with the solution of
 |
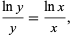(2) |
which is given by
![y={exp[-W_(-1)(-(lnx)/x)] for 1<x<e; exp[-W(-(lnx)/x)] for x>e,](https://mathworld.wolfram.com/images/equations/PowerEquation/NumberedEquation3.gif) |
(3) |
where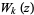 
is the Lambert W-function. This function is illustrated above by the blue curve.
Rational parametric solutions are given by
 |
 |
 |
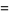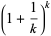(4) |
 |
 |
 |
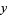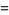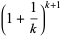(5) |
for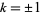 
, 
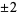, ... (Dunn 1980, Pickover 2002). These solutions are shown on the plot as red dots.
REFERENCES:
Dunn, A. Mathematical Bafflers. New York: Dover, p. 213, 1980.
Pickover, C. A. "The Gaps of Omicron." Ch. 23 in The Mathematics of Oz: Mental Gymnastics from Beyond the Edge. New York: Cambridge University Press, pp. 53-54 and 265, 2002.
|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
