


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-8-2018
Date: 20-9-2019
Date: 19-5-2018
|
Let 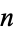 be an integer such that
be an integer such that 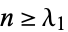 , where
, where 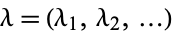 is a partition of
is a partition of 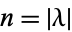 if
if 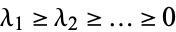 , where
, where 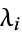 are a sequence of positive integers stabilizing 0 such that
are a sequence of positive integers stabilizing 0 such that 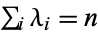 . Also let
. Also let 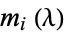 be the number of parts of
be the number of parts of 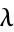 of size
of size 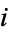 . Then the permutation
. Then the permutation 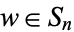 , where
, where 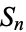 is the symmetric group, acts on the variables
is the symmetric group, acts on the variables 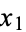 , ...,
, ..., 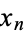 by sending
by sending 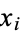 to
to 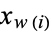 . Letting
. Letting 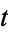 be a complex number, the Hall-Littlewood polynomials are defined by
be a complex number, the Hall-Littlewood polynomials are defined by
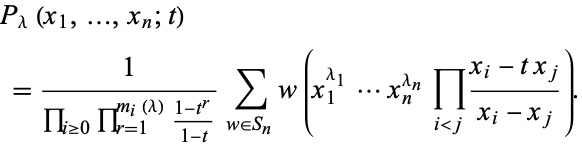 |
These polynomials interpolate between the Schur functions (with 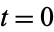 ) and the monomial symmetric functions (with
) and the monomial symmetric functions (with 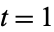 ; Fulman 1999).
; Fulman 1999).
REFERENCES:
Fulman, J. "The Rogers-Ramanujan Identities, the Finite General Linear Groups, and the Hall-Littlewood Polynomials." Proc. Amer. Math. Soc. 128, 17-25, 1999.
Macdonald, I. G. Symmetric Functions and Hall Polynomials, 2nd ed. Oxford, England: Oxford University Press, p. 208, 1995.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|